Surface code offers robust error correction with lower physical qubit requirements, while color code provides greater computational flexibility due to its transversal gate implementations. Explore the rest of the article to understand how these quantum error-correcting codes impact your quantum computing applications.
Table of Comparison
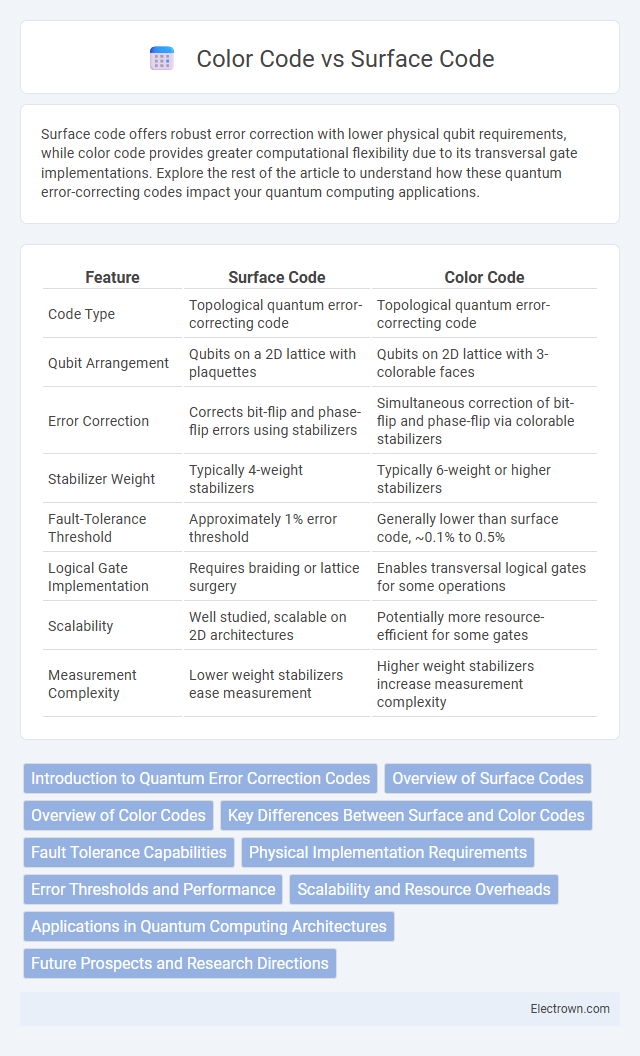
| Feature | Surface Code | Color Code |
|---|---|---|
| Code Type | Topological quantum error-correcting code | Topological quantum error-correcting code |
| Qubit Arrangement | Qubits on a 2D lattice with plaquettes | Qubits on 2D lattice with 3-colorable faces |
| Error Correction | Corrects bit-flip and phase-flip errors using stabilizers | Simultaneous correction of bit-flip and phase-flip via colorable stabilizers |
| Stabilizer Weight | Typically 4-weight stabilizers | Typically 6-weight or higher stabilizers |
| Fault-Tolerance Threshold | Approximately 1% error threshold | Generally lower than surface code, ~0.1% to 0.5% |
| Logical Gate Implementation | Requires braiding or lattice surgery | Enables transversal logical gates for some operations |
| Scalability | Well studied, scalable on 2D architectures | Potentially more resource-efficient for some gates |
| Measurement Complexity | Lower weight stabilizers ease measurement | Higher weight stabilizers increase measurement complexity |
Introduction to Quantum Error Correction Codes
Quantum error correction codes are essential for preserving quantum information against decoherence and operational errors. Surface codes utilize a two-dimensional lattice of qubits with stabilizer measurements focused on plaquettes and stars, providing high error thresholds and topological protection. Color codes extend this structure by using trivalent lattices with colored faces, enabling transversal implementation of a larger set of logical gates and fault-tolerant operations.
Overview of Surface Codes
Surface codes are a class of topological quantum error-correcting codes that use a two-dimensional lattice of qubits arranged on a planar surface to protect quantum information from errors. They leverage local stabilizer measurements corresponding to plaquettes and vertices, enabling high fault-tolerance thresholds near 1%. Widely used in quantum computing architectures, surface codes offer scalable error correction with relatively simple physical implementations compared to other codes like color codes.
Overview of Color Codes
Color codes are a type of topological quantum error-correcting code that generalizes the surface code by using trivalent lattices, enabling transversal implementation of the full Clifford group. They are defined on 2D or 3D lattices with colored plaquettes that facilitate error detection and correction through multi-qubit stabilizer measurements. Color codes provide enhanced fault-tolerance capabilities and offer more efficient logical gate operations compared to traditional surface codes, making them promising for scalable quantum computing architectures.
Key Differences Between Surface and Color Codes
Surface codes and color codes are both topological quantum error-correcting codes but differ primarily in lattice structure and fault-tolerance properties. Surface codes utilize a square lattice with qubits arranged on edges, offering simpler implementation and high error thresholds, while color codes employ a trivalent lattice with qubits on vertices, enabling transversal implementation of a broader set of logical gates. Your choice between these codes depends on balancing code complexity, gate transversality, and error correction performance for quantum computing applications.
Fault Tolerance Capabilities
Surface codes exhibit high fault tolerance due to their ability to efficiently detect and correct local errors using stabilizer measurements on a 2D lattice, achieving error thresholds around 1%. Color codes offer enhanced fault tolerance by supporting transversal implementation of the entire Clifford group, enabling more complex logical gate operations with fewer error propagation risks and thresholds comparable to surface codes, typically near 0.1%-1%. The choice between surface and color codes depends on the specific quantum architecture, as surface codes excel in simplicity and hardware compatibility, while color codes provide greater fault tolerance versatility for universal quantum computation.
Physical Implementation Requirements
Surface codes require a 2D array of qubits with nearest-neighbor interactions, making them compatible with existing superconducting and trapped-ion platforms that allow precise control over local gates and measurements. Color codes demand more complex lattice structures with higher connectivity among qubits, often necessitating 3D layouts or non-planar arrangements that increase physical implementation challenges. The simpler topology and error-correction cycles of surface codes typically result in lower hardware overhead and easier scalability compared to color codes.
Error Thresholds and Performance
Surface codes exhibit high error thresholds around 1%, making them highly resilient to physical qubit errors in quantum computing. Color codes generally offer slightly lower error thresholds, approximately 0.1% to 0.3%, but enable transversal implementation of a broader set of logical gates, enhancing fault-tolerant computational performance. The trade-off between surface codes' superior error tolerance and color codes' gate versatility directly impacts the choice of code for scalable fault-tolerant quantum architectures.
Scalability and Resource Overheads
Surface code exhibits superior scalability due to its two-dimensional lattice structure, enabling efficient error correction with relatively low qubit overhead compared to color code. Color code, while offering transversal logical gate advantages, demands higher resource overheads because of its more complex lattice and increased stabilizer measurements. Consequently, surface code is favored in large-scale quantum computing implementations where minimizing qubit usage and maximizing fault tolerance are critical.
Applications in Quantum Computing Architectures
Surface codes enable robust quantum error correction by encoding logical qubits on a 2D lattice of physical qubits, making them highly suitable for scalable fault-tolerant quantum computing architectures. Color codes extend this approach by allowing transversal implementation of a broader set of logical gates, enhancing computational efficiency in quantum processors. Their complementary strengths drive advancements in designing hybrid quantum architectures that balance error resilience and gate set completeness.
Future Prospects and Research Directions
Surface code demonstrates strong scalability and error tolerance, making it a leading candidate for near-term quantum error correction in superconducting qubit systems. Color code offers advantages in transversal gate implementation and fault-tolerant logical operations, promising more efficient quantum algorithms in the long run. Researchers are exploring hybrid approaches combining both codes to optimize error thresholds and gate complexity, enhancing Your quantum computing capabilities for future applications.
surface code vs color code Infographic
 electrown.com
electrown.com