The master equation governs the time evolution of a quantum system's density matrix, accounting for open system dynamics and interactions with the environment, whereas the Schrodinger equation describes the unitary evolution of a closed system's wavefunction. To understand how these fundamental equations impact your study of quantum mechanics, delve into the rest of this article.
Table of Comparison
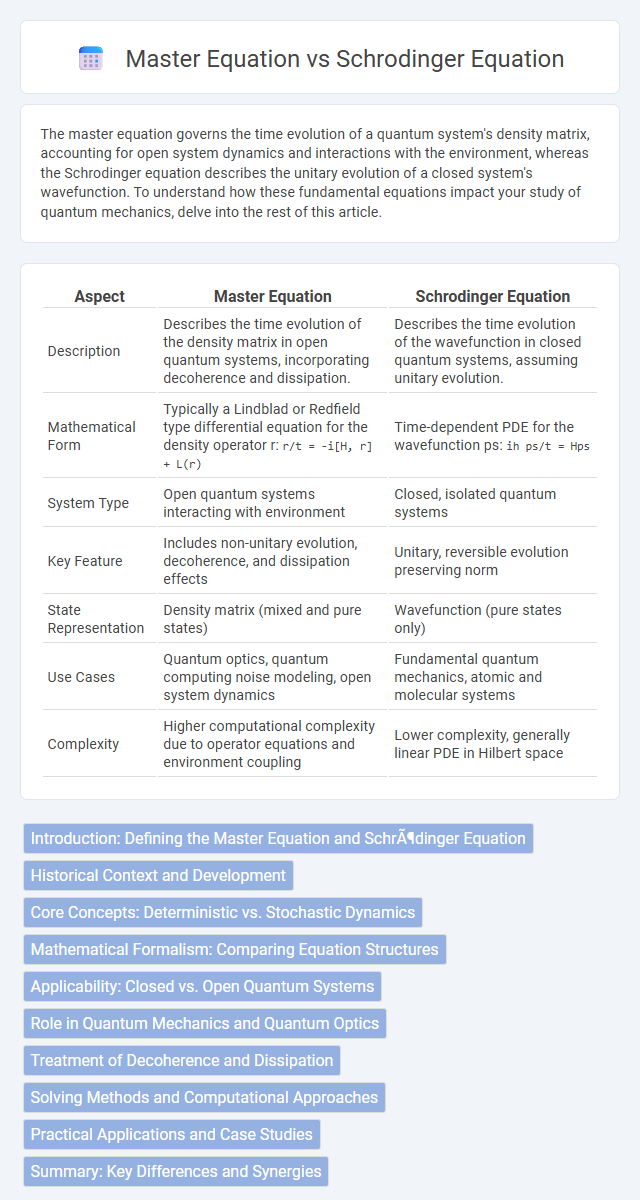
| Aspect | Master Equation | Schrodinger Equation |
|---|---|---|
| Description | Describes the time evolution of the density matrix in open quantum systems, incorporating decoherence and dissipation. | Describes the time evolution of the wavefunction in closed quantum systems, assuming unitary evolution. |
| Mathematical Form | Typically a Lindblad or Redfield type differential equation for the density operator r: r/t = -i[H, r] + L(r) |
Time-dependent PDE for the wavefunction ps: ih ps/t = Hps |
| System Type | Open quantum systems interacting with environment | Closed, isolated quantum systems |
| Key Feature | Includes non-unitary evolution, decoherence, and dissipation effects | Unitary, reversible evolution preserving norm |
| State Representation | Density matrix (mixed and pure states) | Wavefunction (pure states only) |
| Use Cases | Quantum optics, quantum computing noise modeling, open system dynamics | Fundamental quantum mechanics, atomic and molecular systems |
| Complexity | Higher computational complexity due to operator equations and environment coupling | Lower complexity, generally linear PDE in Hilbert space |
Introduction: Defining the Master Equation and Schrödinger Equation
The Schrodinger equation governs the quantum state evolution of closed systems, describing wavefunction dynamics through a deterministic, linear partial differential equation. The master equation extends this framework to open quantum systems by modeling the time evolution of the density matrix, incorporating decoherence and dissipative processes. While the Schrodinger equation applies to pure states, the master equation handles mixed states and environmental interactions key to realistic quantum dynamics.
Historical Context and Development
The Schrodinger equation, formulated by Erwin Schrodinger in 1926, laid the foundation for wave mechanics and quantum mechanics by describing the time evolution of a quantum system's wavefunction. The master equation emerged later as a tool to describe the statistical behavior of open quantum systems interacting with their environment, addressing limitations of the Schrodinger equation in non-isolated scenarios. Understanding your quantum system's dynamics involves choosing between the deterministic Schrodinger equation and the probabilistic master equation, depending on whether environmental interactions are significant.
Core Concepts: Deterministic vs. Stochastic Dynamics
The Schrodinger equation describes deterministic quantum dynamics, providing a precise evolution of the wavefunction over time in closed systems. In contrast, the master equation governs stochastic dynamics by modeling the density matrix's probabilistic evolution, capturing open system interactions and decoherence effects. You rely on the Schrodinger equation for isolated quantum states, while the master equation is essential for systems influenced by environmental noise.
Mathematical Formalism: Comparing Equation Structures
The master equation governs the time evolution of the density matrix, incorporating dissipative processes through Lindblad operators in a generally non-unitary framework. The Schrodinger equation describes the unitary time evolution of the wavefunction using a Hermitian Hamiltonian operator, emphasizing pure quantum states in a closed system. While the Schrodinger equation is a first-order partial differential equation in time for state vectors, the master equation is a linear differential equation for density matrices, capturing open quantum system dynamics and decoherence effects.
Applicability: Closed vs. Open Quantum Systems
The Schrodinger equation describes the deterministic evolution of pure quantum states in closed quantum systems with no interaction with the environment. In contrast, the master equation governs the dynamics of open quantum systems, incorporating decoherence and dissipation due to environmental interactions, enabling modeling of mixed states and non-unitary evolution. This distinction makes the master equation essential for realistic quantum systems exposed to noise and external perturbations, while the Schrodinger equation applies primarily to ideal, isolated systems.
Role in Quantum Mechanics and Quantum Optics
The master equation governs the time evolution of the density matrix in open quantum systems, capturing decoherence and dissipation effects essential for modeling realistic quantum environments. The Schrodinger equation describes the deterministic evolution of pure quantum states, providing a fundamental framework for isolated quantum systems. In quantum optics, the master equation enables analysis of photon interactions and cavity quantum electrodynamics, while the Schrodinger equation underpins wavefunction dynamics in idealized scenarios.
Treatment of Decoherence and Dissipation
The master equation explicitly incorporates decoherence and dissipation by modeling the open quantum system's interaction with its environment, often described through density matrices and Lindblad operators. In contrast, the Schrodinger equation is limited to closed systems, evolving pure states without accounting for environmental noise or energy loss. Consequently, master equations provide a more accurate framework for studying real-world quantum systems where decoherence and dissipation are significant.
Solving Methods and Computational Approaches
The master equation, often used in open quantum systems, is solved using numerical techniques such as the quantum trajectory method, matrix product states, and Lindblad form approximations, enabling efficient handling of dissipative dynamics and decoherence. The Schrodinger equation, central to closed quantum systems, relies primarily on analytical solutions for simple potentials and numerical methods including finite difference methods, spectral methods, and time-dependent density functional theory (TDDFT) to simulate wavefunction evolution. Computational approaches for both equations leverage high-performance computing and tensor network algorithms to address high-dimensional Hilbert spaces and ensure scalable, accurate simulations.
Practical Applications and Case Studies
The Master Equation is widely applied in quantum optics and open quantum systems to model environmental interactions and decoherence, essential for quantum computing error correction and quantum thermodynamics. The Schrodinger Equation governs closed quantum systems' dynamics, fundamental in molecular modeling and quantum chemistry for predicting energy levels and wavefunction evolution. Your choice between these equations depends on whether the system is isolated or interacts with its surroundings, directly impacting practical simulations and experimental designs.
Summary: Key Differences and Synergies
The master equation describes the time evolution of the density matrix in open quantum systems, capturing dissipative processes and decoherence, whereas the Schrodinger equation governs the unitary evolution of pure quantum states in closed systems. You can use the Schrodinger equation for isolated quantum systems where dynamics are coherent, while the master equation is essential for modeling realistic environments interacting with quantum states. Together, these equations provide a comprehensive framework for analyzing both isolated quantum dynamics and environment-induced effects in quantum mechanics.
master equation vs Schrödinger equation Infographic
 electrown.com
electrown.com