Canonical quantization transforms classical fields into operators following commutation relations, providing a framework closely tied to Hamiltonian mechanics, while path integral quantization formulates quantum mechanics through integrals over all possible field configurations, emphasizing the sum-over-histories approach. Understanding the distinctions and applications of these methods can enhance your grasp of quantum field theory; explore the full article to delve deeper into their comparative advantages and use cases.
Table of Comparison
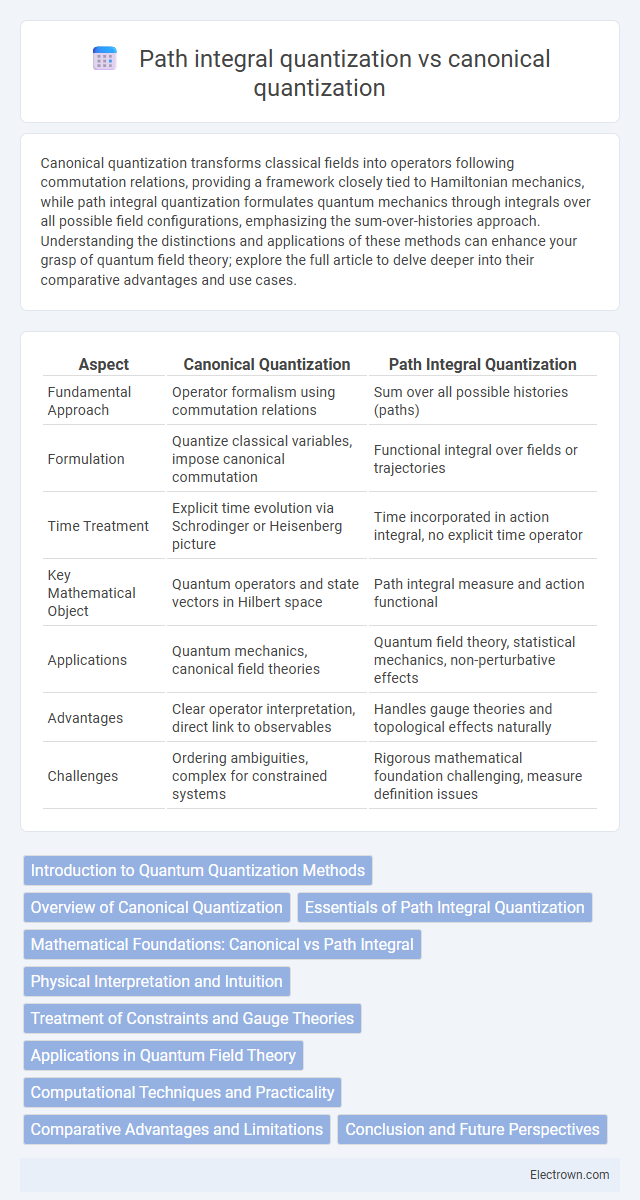
| Aspect | Canonical Quantization | Path Integral Quantization |
|---|---|---|
| Fundamental Approach | Operator formalism using commutation relations | Sum over all possible histories (paths) |
| Formulation | Quantize classical variables, impose canonical commutation | Functional integral over fields or trajectories |
| Time Treatment | Explicit time evolution via Schrodinger or Heisenberg picture | Time incorporated in action integral, no explicit time operator |
| Key Mathematical Object | Quantum operators and state vectors in Hilbert space | Path integral measure and action functional |
| Applications | Quantum mechanics, canonical field theories | Quantum field theory, statistical mechanics, non-perturbative effects |
| Advantages | Clear operator interpretation, direct link to observables | Handles gauge theories and topological effects naturally |
| Challenges | Ordering ambiguities, complex for constrained systems | Rigorous mathematical foundation challenging, measure definition issues |
Introduction to Quantum Quantization Methods
Canonical quantization transforms classical phase space variables into operators that satisfy commutation relations, forming the foundation of operator-based quantum mechanics. Path integral quantization, developed by Feynman, represents quantum amplitudes as sums over all possible histories weighted by the exponential of the action, facilitating non-perturbative and gauge theory analyses. Both methods provide complementary frameworks essential for understanding quantum field theory and particle physics phenomena.
Overview of Canonical Quantization
Canonical quantization transforms classical fields or systems into operators on a Hilbert space by promoting classical variables and Poisson brackets to operators and commutators, respectively. It provides a systematic procedure to impose quantum commutation relations consistent with classical dynamics, enabling the study of time evolution and observables. Your understanding of quantum field theories benefits significantly from mastering canonical quantization as it forms the foundation for many quantum mechanical models.
Essentials of Path Integral Quantization
Path integral quantization formulates quantum mechanics by summing over all possible paths weighted by the exponential of the classical action, providing a probabilistic framework rooted in the principle of least action. This approach captures quantum fluctuations naturally and excels in handling fields and topological effects that are cumbersome in canonical quantization. It facilitates computations of transition amplitudes and correlation functions through functional integrals, enabling a seamless connection to statistical mechanics and perturbative techniques in quantum field theory.
Mathematical Foundations: Canonical vs Path Integral
Canonical quantization relies on promoting classical phase space variables to operators obeying commutation relations derived from Poisson brackets, establishing a Hilbert space framework for quantum states. Path integral quantization formulates quantum mechanics through a sum over all possible classical trajectories weighted by the exponential of the action, relying on functional integration and measure theory in an infinite-dimensional space. While canonical quantization provides operator-based analysis rooted in Hamiltonian formalism, path integral quantization offers a Lagrangian perspective emphasizing global spacetime symmetries and perturbative expansions.
Physical Interpretation and Intuition
Canonical quantization interprets quantum fields as operators acting on a Hilbert space, providing a direct correspondence to classical variables, which offers clear physical intuition through quantized observables and commutation relations. Path integral quantization, on the other hand, provides a probabilistic interpretation by summing over all possible field configurations, emphasizing the quantum behavior as a superposition of histories with weights given by the action's exponential. Your understanding deepens by recognizing canonical quantization's focus on quantized states versus the path integral's holistic approach to quantum amplitudes via functional integration.
Treatment of Constraints and Gauge Theories
Canonical quantization addresses constraints in gauge theories by explicitly imposing constraint conditions on the phase space variables and employing Dirac brackets to handle first-class constraints. Path integral quantization incorporates constraints through the Faddeev-Popov procedure or BRST quantization, introducing ghost fields that systematically account for gauge redundancy in the functional integral. The path integral framework is often more flexible for non-perturbative effects and topological considerations in gauge theories.
Applications in Quantum Field Theory
Canonical quantization is widely used in quantum field theory for systems with well-defined Hamiltonians, enabling straightforward derivation of commutation relations and particle creation and annihilation operators. Path integral quantization excels in gauge theories and non-perturbative calculations, providing a flexible framework to compute correlation functions and transition amplitudes through functional integrals over field configurations. Your choice between these methods depends on the specific quantum field theory problem, balancing computational feasibility with physical insight.
Computational Techniques and Practicality
Canonical quantization relies on operator algebra and commutation relations, making it well-suited for systems with clear Hamiltonian formulations and facilitating the use of canonical commutation techniques. Path integral quantization employs functional integrals over field configurations, providing a versatile framework for gauge theories and non-perturbative computations, often implemented through lattice methods and Monte Carlo simulations. The computational practicality of path integrals stems from their adaptability to numerical methods, while canonical quantization offers clearer operator interpretations but can become cumbersome in strongly interacting or constrained systems.
Comparative Advantages and Limitations
Canonical quantization offers a straightforward approach by promoting classical observables to operators, facilitating the analysis of quantum systems with well-defined canonical coordinates and momenta. Path integral quantization excels in handling systems with complex constraints and topological features, providing a manifestly covariant formalism ideal for gauge theories and quantum field theory. However, canonical quantization struggles with gauge fixing and nontrivial field configurations, while path integral methods face challenges in rigorous mathematical foundations and convergence issues.
Conclusion and Future Perspectives
Canonical quantization and path integral quantization each offer robust frameworks for formulating quantum field theories, with canonical approaches emphasizing operator methods and path integrals providing a sum-over-histories perspective. Your choice of method hinges on the specific problem, computational convenience, and the nature of interactions being studied. Future research aims to unify these techniques with advanced quantum computing algorithms and explore their applications in non-perturbative regimes and quantum gravity.
canonical quantization vs path integral quantization Infographic
 electrown.com
electrown.com