The Bloch sphere represents the state of a single qubit in quantum computing, visualizing quantum superposition and phase relationships on a unit sphere, while the Poincare sphere describes the polarization states of light waves in classical optics, illustrating the orientation and ellipticity of polarization. Explore the rest of the article to understand how these two spheres relate and differ in their applications to your studies or research.
Table of Comparison
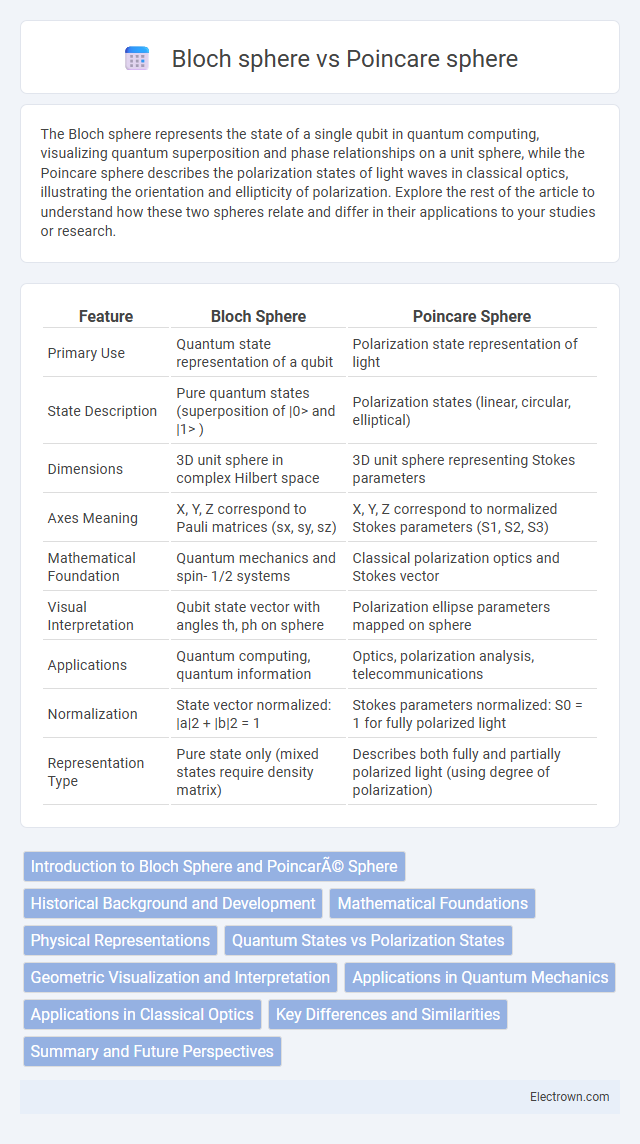
| Feature | Bloch Sphere | Poincare Sphere |
|---|---|---|
| Primary Use | Quantum state representation of a qubit | Polarization state representation of light |
| State Description | Pure quantum states (superposition of |0> and |1> ) | Polarization states (linear, circular, elliptical) |
| Dimensions | 3D unit sphere in complex Hilbert space | 3D unit sphere representing Stokes parameters |
| Axes Meaning | X, Y, Z correspond to Pauli matrices (sx, sy, sz) | X, Y, Z correspond to normalized Stokes parameters (S1, S2, S3) |
| Mathematical Foundation | Quantum mechanics and spin- 1/2 systems | Classical polarization optics and Stokes vector |
| Visual Interpretation | Qubit state vector with angles th, ph on sphere | Polarization ellipse parameters mapped on sphere |
| Applications | Quantum computing, quantum information | Optics, polarization analysis, telecommunications |
| Normalization | State vector normalized: |a|2 + |b|2 = 1 | Stokes parameters normalized: S0 = 1 for fully polarized light |
| Representation Type | Pure state only (mixed states require density matrix) | Describes both fully and partially polarized light (using degree of polarization) |
Introduction to Bloch Sphere and Poincaré Sphere
The Bloch sphere is a geometric representation of the pure state space of a two-level quantum system, commonly used in quantum computing and quantum information theory. The Poincare sphere represents the state of polarization in classical optics, visualizing polarized light states as points on a sphere. Both spheres utilize a three-dimensional vector model to describe the state space, but the Bloch sphere applies to quantum qubits while the Poincare sphere models classical electromagnetic wave polarization.
Historical Background and Development
The Bloch sphere, introduced by Felix Bloch in 1946, serves as a fundamental tool in quantum mechanics to represent the state of a two-level quantum system, such as a qubit. The Poincare sphere, developed earlier by Henri Poincare in 1892, graphically represents the polarization states of light in classical optics. Your understanding of quantum and classical state representations benefits from recognizing the distinct historical roles these spheres have played in advancing their respective fields.
Mathematical Foundations
The Bloch sphere represents the state space of a two-level quantum system using complex projective Hilbert space and SU(2) Lie group symmetry, parametrizing qubit states as points on a unit 3D sphere via spherical coordinates. The Poincare sphere describes polarization states of classical electromagnetic waves, based on Stokes parameters and the SO(3) rotation group, mapping polarization states to points on a unit sphere through normalized intensity differences. Both spheres use spherical geometry for state representation but arise from distinct mathematical frameworks: quantum state vectors in complex Hilbert space versus classical polarization vectors in real Euclidean space.
Physical Representations
The Bloch sphere represents quantum states of a single qubit as points on a unit sphere, with the poles corresponding to computational basis states and the surface encoding superpositions. The Poincare sphere depicts the polarization states of classical light, where points describe elliptical, linear, and circular polarizations based on Stokes parameters. Understanding these physical representations helps you visualize quantum information processing versus classical polarization phenomena effectively.
Quantum States vs Polarization States
The Bloch sphere provides a geometric representation of quantum states of a two-level system, such as a qubit, capturing superposition and phase information critical for quantum computing. In contrast, the Poincare sphere represents polarization states of classical light waves, illustrating the orientation and ellipticity of polarization without quantum properties. Understanding the distinctions between these spheres helps you analyze quantum coherence in qubits versus classical polarization behavior in optics.
Geometric Visualization and Interpretation
The Bloch sphere provides a geometric representation of a single qubit's quantum state, mapping it onto points on a unit sphere to visualize superposition and phase in quantum computing. The Poincare sphere similarly represents the state of polarization of light, using points on a sphere to depict the Stokes parameters and polarization ellipse orientation in classical optics. Both spheres serve as crucial tools for geometric interpretation, enabling intuitive understanding of complex state spaces through three-dimensional visualization of abstract quantum and polarization states.
Applications in Quantum Mechanics
The Bloch sphere provides a geometric representation of a qubit's state in quantum computing, enabling visualization of superposition and quantum gate operations essential for quantum computation and information processing. The Poincare sphere is primarily used in classical and quantum optics to describe polarization states of light, helping analyze and manipulate photon polarization in quantum communication and cryptography. Understanding these spheres enhances your ability to model quantum states and polarization phenomena critical for developing quantum technologies.
Applications in Classical Optics
The Bloch sphere and Poincare sphere are fundamental tools for representing states in different physical contexts, with the Poincare sphere specifically adapted for classical optics to describe polarization states of light. Your understanding of polarization manipulation and measurement benefits from the Poincare sphere's ability to visually map ellipticity, orientation, and degree of polarization, enabling precise control in optical communications and imaging systems. While the Bloch sphere is primarily used in quantum mechanics for qubit state representation, the Poincare sphere remains indispensable in classical optics for analyzing and designing polarization-dependent devices and experiments.
Key Differences and Similarities
The Bloch sphere and Poincare sphere both provide geometric representations of two-state quantum systems, with the Bloch sphere mainly used for qubits in quantum computing and the Poincare sphere for polarization states in optics. Each sphere maps complex state vectors onto points on a unit sphere, enabling visualization of system states through angles corresponding to phase and amplitude. Your understanding deepens by recognizing that while both use similar mathematical frameworks, their applications differ significantly in quantum information science versus classical and quantum polarization analysis.
Summary and Future Perspectives
The Bloch sphere represents quantum states of a single qubit using a three-dimensional unit sphere, providing an intuitive visualization for quantum computing and information processing. The Poincare sphere similarly maps polarization states of light in classical optics, facilitating advances in photonics and polarization-based communication. Future perspectives include leveraging these spheres to enhance quantum error correction, optimize polarization control in optical devices, and develop integrated quantum-photonic systems that unify quantum and classical state representations for improved information technologies.
Bloch sphere vs Poincaré sphere Infographic
 electrown.com
electrown.com