Quantum capacitance arises from the density of states in low-dimensional systems and reflects the ability of electrons to occupy energy levels, whereas classical capacitance depends solely on the physical geometry and dielectric properties of the capacitor. Understanding the differences between quantum and classical capacitance is crucial for optimizing nanoscale electronic devices, so continue reading to explore how these concepts impact your circuit design.
Table of Comparison
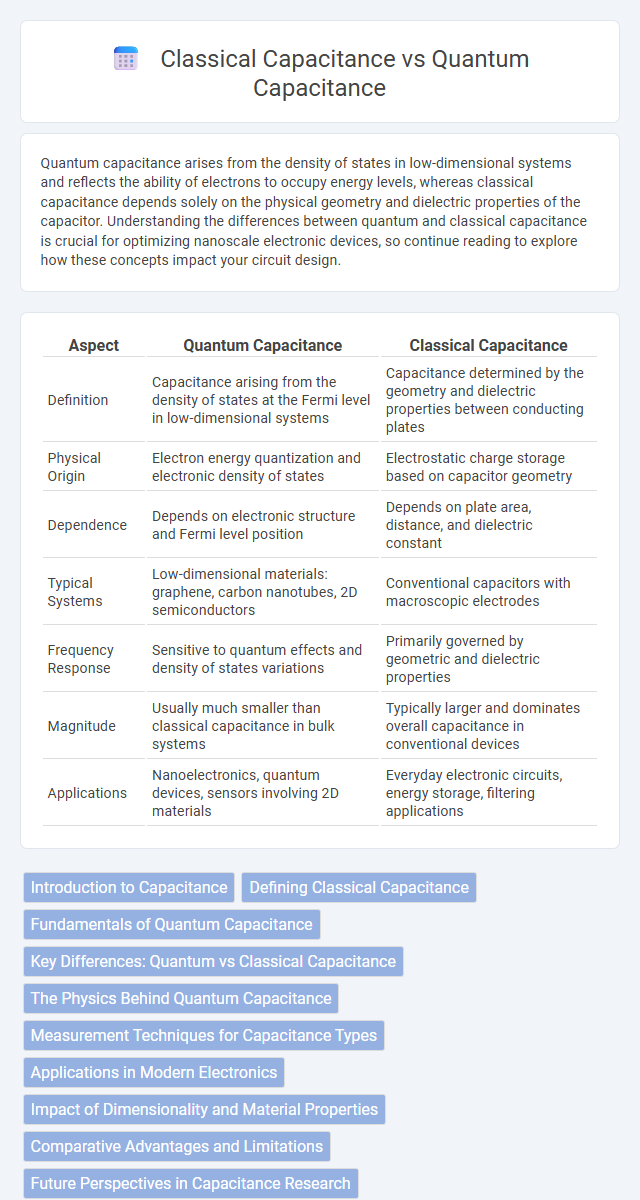
| Aspect | Quantum Capacitance | Classical Capacitance |
|---|---|---|
| Definition | Capacitance arising from the density of states at the Fermi level in low-dimensional systems | Capacitance determined by the geometry and dielectric properties between conducting plates |
| Physical Origin | Electron energy quantization and electronic density of states | Electrostatic charge storage based on capacitor geometry |
| Dependence | Depends on electronic structure and Fermi level position | Depends on plate area, distance, and dielectric constant |
| Typical Systems | Low-dimensional materials: graphene, carbon nanotubes, 2D semiconductors | Conventional capacitors with macroscopic electrodes |
| Frequency Response | Sensitive to quantum effects and density of states variations | Primarily governed by geometric and dielectric properties |
| Magnitude | Usually much smaller than classical capacitance in bulk systems | Typically larger and dominates overall capacitance in conventional devices |
| Applications | Nanoelectronics, quantum devices, sensors involving 2D materials | Everyday electronic circuits, energy storage, filtering applications |
Introduction to Capacitance
Capacitance measures a system's ability to store electric charge per unit voltage, traditionally described by classical capacitance derived from geometric and dielectric properties. Quantum capacitance arises from the finite density of states in low-dimensional materials, reflecting the energy cost of adding electrons at the quantum level. Unlike classical capacitance, quantum capacitance becomes significant in nanoscale devices where electronic states limit charge storage capacity.
Defining Classical Capacitance
Classical capacitance is defined as the ability of a system to store electric charge, determined by the physical geometry and dielectric properties of the capacitor, typically calculated using the formula C = eA/d. Unlike quantum capacitance, which arises from electron density of states and energy quantization effects at the nanoscale, classical capacitance depends solely on macroscopic parameters such as electrode area, separation distance, and permittivity of the insulating material. Understanding classical capacitance is essential for designing traditional capacitors and serves as a baseline when exploring quantum effects in nanoelectronics and advanced materials.
Fundamentals of Quantum Capacitance
Quantum capacitance arises from the finite density of electronic states in low-dimensional materials, reflecting the energy cost to add electrons to a quantum system. Unlike classical capacitance, which depends solely on geometric factors and dielectric properties, quantum capacitance depends on the electronic structure and band filling of the material. It becomes significant in nanoscale devices where electrostatic capacitance is comparable to or smaller than the quantum capacitance, influencing charge storage and transport behavior.
Key Differences: Quantum vs Classical Capacitance
Quantum capacitance arises from the finite density of states at the Fermi level in low-dimensional materials, limiting the charge storage capacity at the nanoscale. Classical capacitance depends primarily on geometric factors and dielectric properties, following the relationship C = eA/d, where e is permittivity, A is area, and d is the separation distance. Your device performance at the quantum scale is influenced by both capacitance types, requiring consideration of quantum capacitance for accurate modeling and enhanced nanoscale energy storage applications.
The Physics Behind Quantum Capacitance
Quantum capacitance arises from the discrete density of states in low-dimensional materials, reflecting the energy required to add electrons to a system. Unlike classical capacitance, which depends solely on geometric factors and dielectric properties, quantum capacitance incorporates electronic band structure and Fermi level shifts. Your understanding of quantum capacitance is crucial for optimizing nanoscale electronic devices where charge quantization and electron interactions dominate.
Measurement Techniques for Capacitance Types
Quantum capacitance measurement employs techniques such as low-temperature transport measurements and scanning tunneling microscopy to probe electron density states and energy band structure at the nanoscale. Classical capacitance is typically measured using impedance spectroscopy, LCR meters, or time-domain reflectometry, which assess charge storage by applying AC signals and analyzing voltage-current relationships. Understanding these methods is crucial for distinguishing intrinsic quantum effects in materials from conventional electrostatic behavior in capacitors.
Applications in Modern Electronics
Quantum capacitance plays a crucial role in modern electronics by enabling ultra-sensitive charge detection and energy storage at the nanoscale, outperforming classical capacitance in devices like graphene-based transistors and quantum dots. Unlike classical capacitance, which depends on geometric factors and dielectric materials, quantum capacitance depends on the electronic density of states, making it essential for the design of next-generation high-speed, low-power electronic components. Applications include advanced sensors, flexible electronics, and quantum computing hardware where precise control of electron behavior is required.
Impact of Dimensionality and Material Properties
Quantum capacitance significantly depends on the dimensionality of the material, as lower-dimensional systems like graphene exhibit reduced density of states, which directly limits their charge storage capacity. Material properties such as electron mobility, effective mass, and dielectric constant modulate quantum capacitance by influencing the energy band structure and density of states at the Fermi level. Unlike classical capacitance, which relies primarily on geometric factors and dielectric permittivity, quantum capacitance is governed by intrinsic electronic properties that become critical in nanoscale and low-dimensional devices.
Comparative Advantages and Limitations
Quantum capacitance offers superior sensitivity in nanoscale and low-dimensional systems due to its dependence on the electronic density of states, enabling enhanced performance in advanced sensors and quantum devices. Classical capacitance, governed by geometric factors and dielectric properties, provides reliable and predictable behavior for traditional circuits but lacks the nuanced responsiveness of quantum capacitance. Your choice between them hinges on the application scale and required precision, where quantum capacitance excels in miniaturized, high-frequency environments and classical capacitance suits larger, more stable systems.
Future Perspectives in Capacitance Research
Quantum capacitance, emerging from charge carrier density variations in low-dimensional materials, offers unparalleled sensitivity in nanoscale electronic devices compared to classical capacitance that relies on geometric factors and dielectric constants. Future research is poised to harness quantum capacitance in ultra-fast transistors, energy storage, and quantum computing, where traditional capacitor models fall short in describing low-dimensional systems. Advancements in materials like graphene and transition metal dichalcogenides will drive the development of hybrid capacitors, optimizing energy density and charge transport beyond classical limitations.
quantum capacitance vs classical capacitance Infographic
 electrown.com
electrown.com