Adiabatic quantum computing relies on slowly evolving the quantum state to solve optimization problems, while gate model quantum computing uses discrete sequences of quantum gates to perform algorithms with high precision. Explore how your choice between these models impacts computational efficiency and problem-solving capabilities in the full article.
Table of Comparison
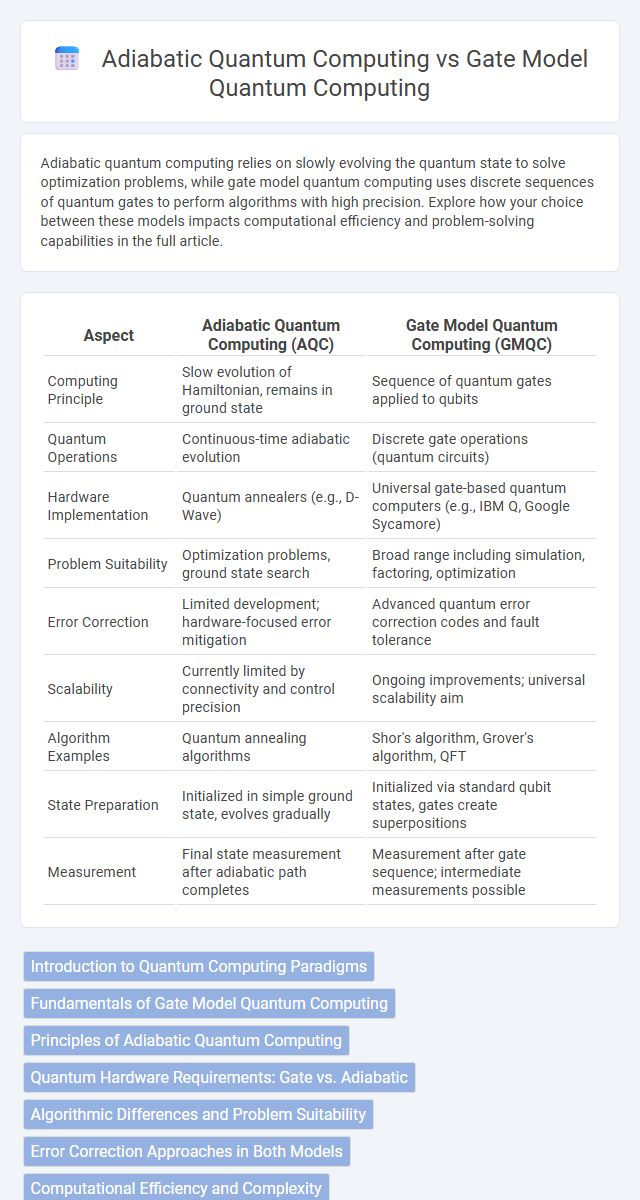
| Aspect | Adiabatic Quantum Computing (AQC) | Gate Model Quantum Computing (GMQC) |
|---|---|---|
| Computing Principle | Slow evolution of Hamiltonian, remains in ground state | Sequence of quantum gates applied to qubits |
| Quantum Operations | Continuous-time adiabatic evolution | Discrete gate operations (quantum circuits) |
| Hardware Implementation | Quantum annealers (e.g., D-Wave) | Universal gate-based quantum computers (e.g., IBM Q, Google Sycamore) |
| Problem Suitability | Optimization problems, ground state search | Broad range including simulation, factoring, optimization |
| Error Correction | Limited development; hardware-focused error mitigation | Advanced quantum error correction codes and fault tolerance |
| Scalability | Currently limited by connectivity and control precision | Ongoing improvements; universal scalability aim |
| Algorithm Examples | Quantum annealing algorithms | Shor's algorithm, Grover's algorithm, QFT |
| State Preparation | Initialized in simple ground state, evolves gradually | Initialized via standard qubit states, gates create superpositions |
| Measurement | Final state measurement after adiabatic path completes | Measurement after gate sequence; intermediate measurements possible |
Introduction to Quantum Computing Paradigms
Adiabatic quantum computing relies on evolving a quantum system slowly to remain in its ground state, solving optimization problems by encoding solutions into the system's lowest energy configuration. Gate model quantum computing utilizes sequences of quantum gates to manipulate qubits through unitary transformations for algorithms like Shor's and Grover's. These paradigms differ in operational principles, with adiabatic focusing on energy landscapes and gate model on circuit-based quantum logic.
Fundamentals of Gate Model Quantum Computing
Gate model quantum computing operates by manipulating qubits through a sequence of quantum gates, which serve as the fundamental building blocks implementing unitary transformations on quantum states. These gates, including Hadamard, CNOT, and phase shift gates, enable the construction of complex quantum circuits that exploit superposition and entanglement for computational advantages. The gate model approach relies on precise control and error correction to maintain coherence and perform algorithms such as Shor's and Grover's, making it distinct from the continuous-time evolution paradigm of adiabatic quantum computing.
Principles of Adiabatic Quantum Computing
Adiabatic Quantum Computing (AQC) relies on the gradual evolution of a quantum system's ground state to solve optimization problems, beginning with a simple Hamiltonian and slowly transforming it into a problem-specific Hamiltonian. This continuous change ensures the system remains in its lowest energy state, encoding the solution at the end of the computation. Your choice between AQC and gate model quantum computing depends on the problem type, as AQC excels in optimization and certain combinatorial challenges through its unique energy-based approach.
Quantum Hardware Requirements: Gate vs. Adiabatic
Adiabatic quantum computing requires hardware capable of precisely controlling slow, continuous variations in Hamiltonian parameters to maintain the system in its ground state, demanding high coherence times and stable qubit connectivity. Gate model quantum computing relies on fast, discrete gate operations with high-fidelity single- and two-qubit gates, necessitating error correction mechanisms due to decoherence and operational errors. Your choice between these models depends on the maturity of available hardware platforms and the specific quantum optimization problems you aim to solve.
Algorithmic Differences and Problem Suitability
Adiabatic quantum computing relies on the gradual evolution of the system's Hamiltonian to find the ground state solution, making it well-suited for optimization problems and combinatorial searches. Gate model quantum computing uses discrete quantum gates to implement algorithms like Shor's or Grover's, providing greater flexibility for complex computations and error-correcting protocols. Your choice depends on whether the problem benefits from energy landscape exploration via adiabatic methods or the structured operations enabling versatile algorithm implementation in gate models.
Error Correction Approaches in Both Models
Error correction in adiabatic quantum computing relies on energy gap protection and robust Hamiltonian design to minimize errors during slow evolution, while gate model quantum computing utilizes quantum error correction codes like the surface code to actively detect and correct qubit errors in real time. The gate model's error correction schemes involve syndrome measurement and fault-tolerant gate implementations, providing scalable pathways for reliable quantum computations. Your choice between these models depends on the error tolerance needs and current technological maturity of error correction protocols.
Computational Efficiency and Complexity
Adiabatic quantum computing leverages gradual Hamiltonian evolution to solve optimization problems, often exhibiting improved performance for specific problem classes by evolving the system into the ground state, potentially reducing computational complexity for those tasks. Gate model quantum computing uses discrete quantum gates to manipulate qubits, enabling universal quantum algorithms but sometimes facing higher overhead due to error correction and circuit depth, impacting computational efficiency. Your choice between these models should consider problem structure, as adiabatic approaches may be more efficient for optimization challenges, whereas gate models excel in general-purpose quantum computations.
Current Implementations and Technological Maturity
Adiabatic quantum computing (AQC) primarily advances through companies like D-Wave Systems, which have developed commercially available quantum annealers focused on optimization problems but with limited gate operation flexibility. Gate model quantum computing, led by IBM, Google, and Rigetti, demonstrates greater technological maturity with universal quantum processors capable of executing diverse quantum algorithms using qubit manipulation and error correction techniques. Your choice between these paradigms depends on the specific application, as AQC offers specialized solutions for certain optimization tasks, while gate model quantum computing aims for broader computational applicability.
Practical Applications and Use Cases
Adiabatic quantum computing excels in optimization problems, such as portfolio optimization, protein folding, and traffic flow management, leveraging its ability to find ground states of complex systems. Gate model quantum computing demonstrates strengths in quantum algorithms like Shor's for factoring and Grover's for search, applicable in cryptography, quantum simulation, and chemistry modeling. Both paradigms offer complementary advantages, with adiabatic methods suited for constrained optimization and gate-based systems better for universal algorithmic processes.
Future Prospects and Research Directions
Adiabatic quantum computing (AQC) shows promise for optimization problems and quantum annealing, leveraging gradual Hamiltonian evolution to remain in the ground state, which may offer robustness against certain types of decoherence. Gate model quantum computing emphasizes universal, fault-tolerant quantum circuits capable of implementing a broad array of algorithms, with ongoing research targeting error correction and scalability. Future research directions focus on hybrid approaches integrating AQC and gate models, development of error mitigation techniques, and exploration of hardware advancements like superconducting qubits and trapped ions for enhanced quantum advantage.
adiabatic quantum computing vs gate model quantum computing Infographic
 electrown.com
electrown.com