Quantum walks enable particles to explore multiple paths simultaneously through superposition, leading to faster spreading and interference effects unlike classical random walks driven by simple probabilistic steps. Discover how these distinctions can revolutionize algorithms and impact computational efficiency by reading the rest of the article.
Table of Comparison
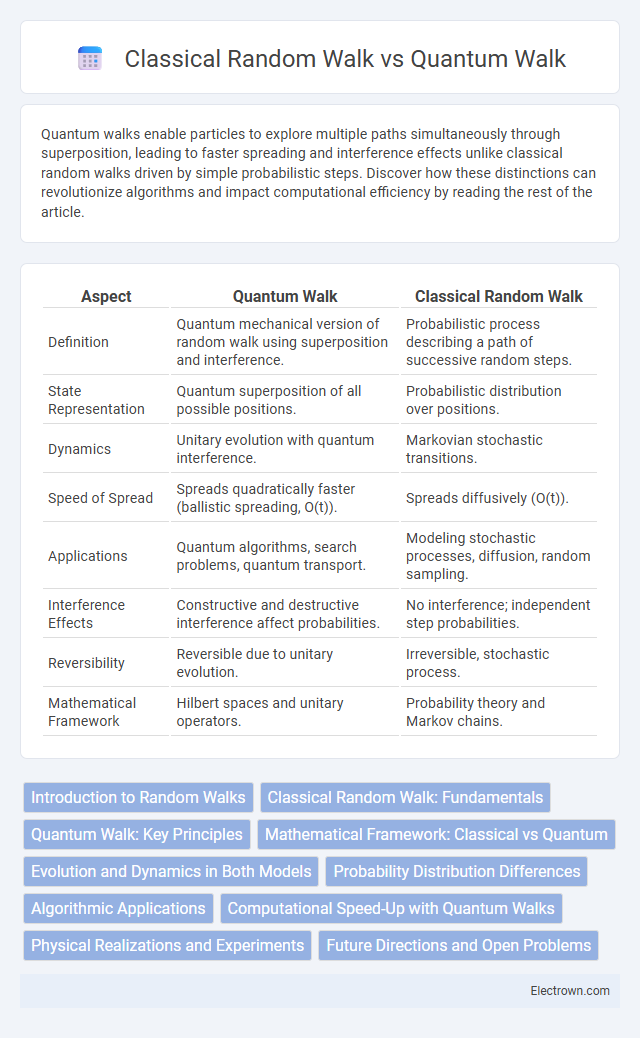
| Aspect | Quantum Walk | Classical Random Walk |
|---|---|---|
| Definition | Quantum mechanical version of random walk using superposition and interference. | Probabilistic process describing a path of successive random steps. |
| State Representation | Quantum superposition of all possible positions. | Probabilistic distribution over positions. |
| Dynamics | Unitary evolution with quantum interference. | Markovian stochastic transitions. |
| Speed of Spread | Spreads quadratically faster (ballistic spreading, O(t)). | Spreads diffusively (O(t)). |
| Applications | Quantum algorithms, search problems, quantum transport. | Modeling stochastic processes, diffusion, random sampling. |
| Interference Effects | Constructive and destructive interference affect probabilities. | No interference; independent step probabilities. |
| Reversibility | Reversible due to unitary evolution. | Irreversible, stochastic process. |
| Mathematical Framework | Hilbert spaces and unitary operators. | Probability theory and Markov chains. |
Introduction to Random Walks
Random walks describe mathematical models where an entity moves step-by-step in random directions, widely applied in physics, computer science, and finance. Classical random walks rely on probabilistic transitions between discrete states, leading to diffusive spreading characterized by linear variance over time. Quantum walks leverage superposition and interference, enabling faster spreading and potential exponential speedups in algorithms compared to classical random walks.
Classical Random Walk: Fundamentals
Classical random walks are stochastic processes where a particle moves step-by-step in a given space, with each step chosen according to fixed probability distributions. These walks exhibit diffusive behavior characterized by a mean squared displacement proportional to time, which leads to slow spreading over the state space. Understanding classical random walk fundamentals helps you appreciate their applications in algorithms, statistical physics, and network theory, forming the baseline for comparison with quantum walks.
Quantum Walk: Key Principles
Quantum walks leverage superposition and interference to explore multiple paths simultaneously, resulting in faster and more efficient exploration than classical random walks. These walks operate on quantum bits (qubits), enabling probability amplitudes to interfere constructively or destructively, dynamically affecting the walk's evolution. Your understanding of quantum computing algorithms can be enhanced by grasping how quantum walks outperform classical random walks in search and optimization tasks.
Mathematical Framework: Classical vs Quantum
The mathematical framework of a classical random walk is characterized by probabilistic transition matrices representing movement between states, governed by Markov chains and described using stochastic matrices. In contrast, quantum walks utilize unitary operators on complex Hilbert spaces, where evolution is determined by quantum amplitudes and interference effects, implemented through coin and shift operators. This fundamental difference results in distinct propagation properties, with classical walks leading to diffusive spreading and quantum walks exhibiting ballistic spreading due to superposition and entanglement.
Evolution and Dynamics in Both Models
Quantum walks exhibit unitary evolution described by quantum superposition and interference, resulting in faster spreading dynamics compared to classical random walks governed by probabilistic transitions. The quantum walk's state vector evolves according to a time-dependent unitary operator, enabling phenomena such as ballistic transport, whereas classical random walks evolve via Markov chains with diffusive behavior. Consequently, quantum walks demonstrate quadratic speedup in mixing and hitting times, essential for quantum algorithms and search processes.
Probability Distribution Differences
Quantum walk probability distributions exhibit pronounced interference patterns resulting in faster spreading and higher peak probabilities compared to the Gaussian-like, diffusive distribution of classical random walks. The quantum walk's probability distribution is often characterized by ballistic transport, leading to a standard deviation scaling linearly with time, whereas classical random walks show a square root time dependence. These distinctions in probability distributions underpin quantum algorithms with quadratic speedups over classical counterparts in search and graph traversal tasks.
Algorithmic Applications
Quantum walks offer exponential speedups over classical random walks in solving graph-based problems, such as element distinctness and triangle finding, by exploiting quantum superposition and interference. Your algorithm can leverage these quantum properties to achieve more efficient search and sampling methods, significantly reducing computational complexity. This advantage makes quantum walks a powerful tool in optimization, database search, and quantum simulation tasks compared to their classical counterparts.
Computational Speed-Up with Quantum Walks
Quantum walks provide a significant computational speed-up over classical random walks by exploiting quantum superposition and interference, enabling faster exploration of complex graph structures. Algorithms utilizing quantum walks can achieve polynomial or even exponential speed-ups in search and optimization problems, reducing the time complexity compared to classical counterparts. Your ability to harness quantum walks enhances solving problems like element distinctness and spatial search, outperforming classical random walk methods.
Physical Realizations and Experiments
Quantum walks have been experimentally realized using trapped ions, photonic systems, and cold atoms, enabling precise control over superposition and interference effects not seen in classical random walks. Physical implementations demonstrate faster spreading and quadratically enhanced hitting times in quantum walks compared to classical counterparts, confirming theoretical predictions. Experiments leveraging optical lattices and integrated photonic circuits showcase the scalability and robustness of quantum walks for quantum computing applications.
Future Directions and Open Problems
Quantum walks exhibit unique interference and superposition properties that offer promising avenues for future research in quantum algorithms and complex network analysis. Open problems include enhancing coherence times, optimizing quantum walk-based search algorithms, and understanding scaling behaviors in higher-dimensional or noisy environments. Your exploration into these aspects could lead to breakthroughs in quantum computation and communication technologies.
quantum walk vs classical random walk Infographic
 electrown.com
electrown.com