Fock states, also known as number states, represent a precise number of photons, exhibiting quantum properties ideal for applications requiring exact photon control, whereas coherent states resemble classical light with well-defined phases and amplitudes, commonly found in lasers. Discover how understanding the differences between these states can enhance Your grasp of quantum optics in the rest of this article.
Table of Comparison
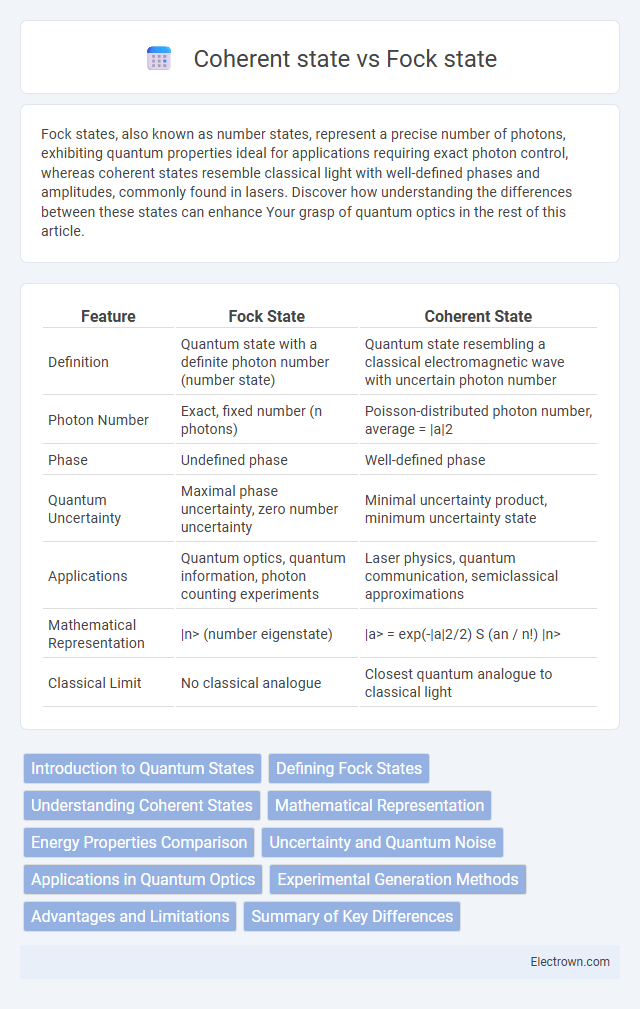
| Feature | Fock State | Coherent State |
|---|---|---|
| Definition | Quantum state with a definite photon number (number state) | Quantum state resembling a classical electromagnetic wave with uncertain photon number |
| Photon Number | Exact, fixed number (n photons) | Poisson-distributed photon number, average |
| Phase | Undefined phase | Well-defined phase |
| Quantum Uncertainty | Maximal phase uncertainty, zero number uncertainty | Minimal uncertainty product, minimum uncertainty state |
| Applications | Quantum optics, quantum information, photon counting experiments | Laser physics, quantum communication, semiclassical approximations |
| Mathematical Representation | |n> (number eigenstate) | |a> = exp(-|a|2/2) S (an / n!) |n> |
| Classical Limit | No classical analogue | Closest quantum analogue to classical light |
Introduction to Quantum States
Fock states, also known as number states, represent quantum states with a well-defined number of particles or photons, crucial for quantized energy level descriptions in quantum mechanics. Coherent states, by contrast, describe quantum states that closely resemble classical oscillations, characterized by a minimum uncertainty product and eigenstates of the annihilation operator. Both are fundamental in quantum optics, with Fock states emphasizing discrete quantization and coherent states enabling semiclassical interpretations of electromagnetic fields.
Defining Fock States
Fock states, also known as number states, are quantum states with a well-defined number of particles or photons, characterized by an exact photon count in a single mode of the electromagnetic field. Unlike coherent states, which resemble classical electromagnetic waves with uncertain photon numbers and Poissonian distribution, Fock states exhibit zero uncertainty in photon number, making them essential for applications requiring precise quantum control. Your understanding of quantum optics benefits from recognizing Fock states as fundamental building blocks for quantum information processing and quantum metrology.
Understanding Coherent States
Coherent states represent quantum states of the electromagnetic field that closely resemble classical light waves, characterized by minimum uncertainty and a well-defined phase. Unlike Fock states, which have a fixed number of photons and are highly nonclassical, coherent states exhibit Poissonian photon number distributions, making them essential in quantum optics and laser physics. Your ability to model and manipulate light using coherent states enables advances in quantum communication and precision measurement technologies.
Mathematical Representation
Fock states, also known as number states, are represented mathematically by |n> , where n denotes the exact number of photons in the quantum mode, characterized by discrete eigenvalues of the number operator \(\hat{n} = \hat{a}^\dagger \hat{a}\). Coherent states |a> are eigenstates of the annihilation operator \(\hat{a}\) with complex eigenvalue a, expressed as a superposition of Fock states weighted by the Poisson distribution, \(|\alpha> = e^{-|\alpha|^2/2} \sum_{n=0}^{\infty} \frac{\alpha^n}{\sqrt{n!}} |n> \). Your choice between these states impacts quantum optics analyses due to their fundamentally different mathematical structures and quantum statistical properties.
Energy Properties Comparison
Fock states exhibit discrete energy levels with a fixed number of photons, making their energy quantized and deterministic. Coherent states possess a Poissonian photon number distribution, leading to a well-defined average energy but with inherent fluctuations. Your choice depends on whether precise energy quantization or average energy stability is more critical in your quantum optics application.
Uncertainty and Quantum Noise
Fock states, characterized by a fixed number of photons, exhibit zero uncertainty in photon number but maximum phase uncertainty, leading to quantum noise dominated by number fluctuations. Coherent states, representing classical-like light, display minimum uncertainty equally distributed between photon number and phase, minimizing quantum noise and resembling classical electromagnetic fields. The balance of uncertainty in coherent states makes them essential for applications requiring low quantum noise, unlike Fock states that are critical in quantum information tasks demanding precise photon number control.
Applications in Quantum Optics
Fock states are essential in quantum optics for precise photon-number-resolving measurements and quantum information processing, enabling deterministic control of single photons in quantum communication protocols. Coherent states, often described as the closest quantum analog to classical light, play a crucial role in laser physics, quantum metrology, and continuous-variable quantum key distribution, offering stable phase and amplitude properties. Both states serve complementary functions in developing quantum technologies, with Fock states providing discrete quantum resources and coherent states enabling robust, easily generated optical fields.
Experimental Generation Methods
Fock states are experimentally generated using single-photon sources such as spontaneous parametric down-conversion (SPDC) and quantum dot emitters, which allow precise control over photon number states. Coherent states are typically produced by attenuated laser fields emitting a well-defined phase and amplitude, characteristic of classical electromagnetic waves. Quantum optical cavities and nonlinear crystals play essential roles in shaping and maintaining both Fock and coherent states during experiments.
Advantages and Limitations
Fock states, characterized by a fixed number of photons, provide precise photon number resolution essential for quantum information processing and metrology, but their generation and detection remain experimentally challenging due to sensitivity to loss and noise. Coherent states offer robust, classical-like light sources with well-defined amplitudes, enabling easy generation and manipulation in quantum optics and communication, although they lack exact photon number certainty and are susceptible to phase noise. Choosing between Fock and coherent states depends on the trade-off between non-classical precision and practical implementation complexity in quantum technology applications.
Summary of Key Differences
Fock states represent quantum states with a fixed number of photons, characterized by discrete energy levels and exact photon number certainty. Coherent states, often described as the closest quantum analog to classical electromagnetic waves, exhibit a Poisson distribution of photon numbers and maintain minimum uncertainty in both amplitude and phase. Understanding these differences helps you select the appropriate state for applications in quantum optics, quantum information, and precision measurements.
Fock state vs coherent state Infographic
 electrown.com
electrown.com