Quantum state tomography reconstructs the complete quantum state of a system using measurements, providing detailed insights into quantum phenomena beyond the reach of classical state estimation techniques that rely only on probability distributions and statistical inference. Explore the rest of the article to understand the critical differences and applications of these methods in modern quantum research.
Table of Comparison
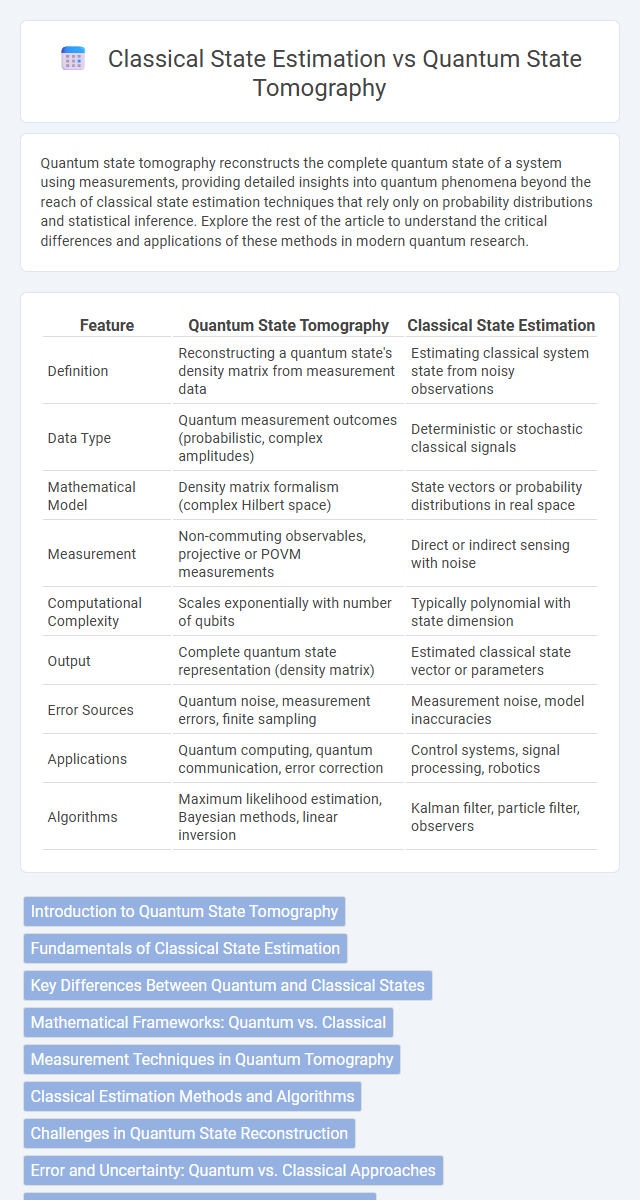
| Feature | Quantum State Tomography | Classical State Estimation |
|---|---|---|
| Definition | Reconstructing a quantum state's density matrix from measurement data | Estimating classical system state from noisy observations |
| Data Type | Quantum measurement outcomes (probabilistic, complex amplitudes) | Deterministic or stochastic classical signals |
| Mathematical Model | Density matrix formalism (complex Hilbert space) | State vectors or probability distributions in real space |
| Measurement | Non-commuting observables, projective or POVM measurements | Direct or indirect sensing with noise |
| Computational Complexity | Scales exponentially with number of qubits | Typically polynomial with state dimension |
| Output | Complete quantum state representation (density matrix) | Estimated classical state vector or parameters |
| Error Sources | Quantum noise, measurement errors, finite sampling | Measurement noise, model inaccuracies |
| Applications | Quantum computing, quantum communication, error correction | Control systems, signal processing, robotics |
| Algorithms | Maximum likelihood estimation, Bayesian methods, linear inversion | Kalman filter, particle filter, observers |
Introduction to Quantum State Tomography
Quantum State Tomography (QST) is a method used to reconstruct the quantum state of a system by performing a series of measurements on multiple copies of the state. Unlike classical state estimation, which deals with probabilities and outcomes in classical systems, QST handles the complexities of quantum mechanics, including superposition and entanglement, by estimating density matrices or wavefunctions. This technique is essential for verifying quantum devices, calibrating quantum gates, and advancing quantum information processing and computation.
Fundamentals of Classical State Estimation
Classical state estimation involves reconstructing a physical system's state by analyzing measurement outcomes to infer parameters describing that system. It relies on statistical methods such as maximum likelihood estimation and Bayesian inference to process noisy or incomplete data, optimizing accuracy. The approach assumes deterministic underlying states, contrasting with quantum state tomography, which must address quantum superposition and entanglement inherent in quantum systems.
Key Differences Between Quantum and Classical States
Quantum state tomography reconstructs the full density matrix representing a quantum system, capturing superposition and entanglement properties that classical state estimation cannot access. Classical state estimation deals with probability distributions over well-defined, mutually exclusive states, lacking the ability to characterize coherence and non-commuting observables. This fundamental difference highlights the quantum state's complex vector space nature versus the classical state's probabilistic simplex structure.
Mathematical Frameworks: Quantum vs. Classical
Quantum state tomography relies on the density matrix formalism and employs operators in Hilbert space to reconstruct quantum states from measurement outcomes, capturing superposition and entanglement properties. Classical state estimation uses probability distributions and statistical inference in phase space to characterize system states, assuming determinism and absence of coherence. The mathematical distinction lies in the non-commutative operator algebra of quantum mechanics versus the commutative probability theory underlying classical estimation.
Measurement Techniques in Quantum Tomography
Measurement techniques in quantum state tomography employ a series of projective measurements or positive operator-valued measures (POVMs) to reconstruct the density matrix of a quantum system, capturing its complete quantum state. Unlike classical state estimation, which relies on direct measurements of observable parameters, quantum tomography requires collecting statistically significant outcomes from multiple bases to overcome the probabilistic nature of quantum mechanics. Your choice of measurement scheme directly impacts the accuracy and efficiency of the quantum state reconstruction process.
Classical Estimation Methods and Algorithms
Classical estimation methods for quantum state tomography rely on statistical techniques such as maximum likelihood estimation (MLE), least squares, and linear inversion to reconstruct the quantum state from measurement data. These algorithms are designed to handle noise and incomplete data, optimizing parameter estimation within the constraints of classical computational resources. Your choice of classical estimation algorithm impacts the accuracy and efficiency of the quantum state reconstruction, influencing downstream quantum information processing tasks.
Challenges in Quantum State Reconstruction
Quantum state tomography faces significant challenges in quantum state reconstruction due to the exponential growth of the Hilbert space with system size, making it computationally intensive compared to classical state estimation. Noise, measurement errors, and limited data further complicate accurate quantum state characterization, requiring sophisticated statistical methods and regularization techniques. Your ability to reconstruct quantum states precisely depends on overcoming these obstacles to achieve reliable quantum information processing and benchmarking.
Error and Uncertainty: Quantum vs. Classical Approaches
Quantum state tomography inherently faces greater uncertainty due to the probabilistic nature of quantum measurements and the no-cloning theorem, which limits repeated measurements on identical states. Classical state estimation benefits from deterministic measurements and often lower noise levels, resulting in more precise parameter extraction with reduced error margins. Error analysis in quantum tomography uses statistical inference methods like maximum likelihood estimation or Bayesian approaches to mitigate uncertainty, but the fundamental quantum noise imposes limits absent in classical systems.
Applications in Quantum and Classical Systems
Quantum state tomography enables precise reconstruction of quantum states, crucial for developing quantum computing algorithms, secure quantum communication, and validating quantum sensors. Classical state estimation techniques are applied widely in signal processing, control systems, and machine learning to predict system behaviors and optimize performance. Both methods enhance system diagnostics, but quantum tomography specifically addresses the probabilistic nature of quantum systems, enabling breakthroughs in quantum information science.
Future Directions in State Estimation Technologies
Future directions in quantum state tomography emphasize enhancing measurement efficiency and scalability to accommodate increasingly complex quantum systems, leveraging machine learning algorithms to improve reconstruction accuracy. Classical state estimation techniques are evolving through integration with real-time data processing and adaptive feedback mechanisms to optimize sensor precision and robustness. Cross-disciplinary approaches combining quantum and classical methodologies aim to develop hybrid frameworks that maximize the strengths of both paradigms for advanced state estimation applications.
quantum state tomography vs classical state estimation Infographic
 electrown.com
electrown.com