Polyphase filters and FIR filters both serve essential roles in digital signal processing, with polyphase filters offering efficient multi-rate processing by decomposing a filter into multiple phases, while FIR filters are prized for their linear phase response and stability. Discover how each filter type can impact Your signal processing projects by reading the full comparison in this article.
Table of Comparison
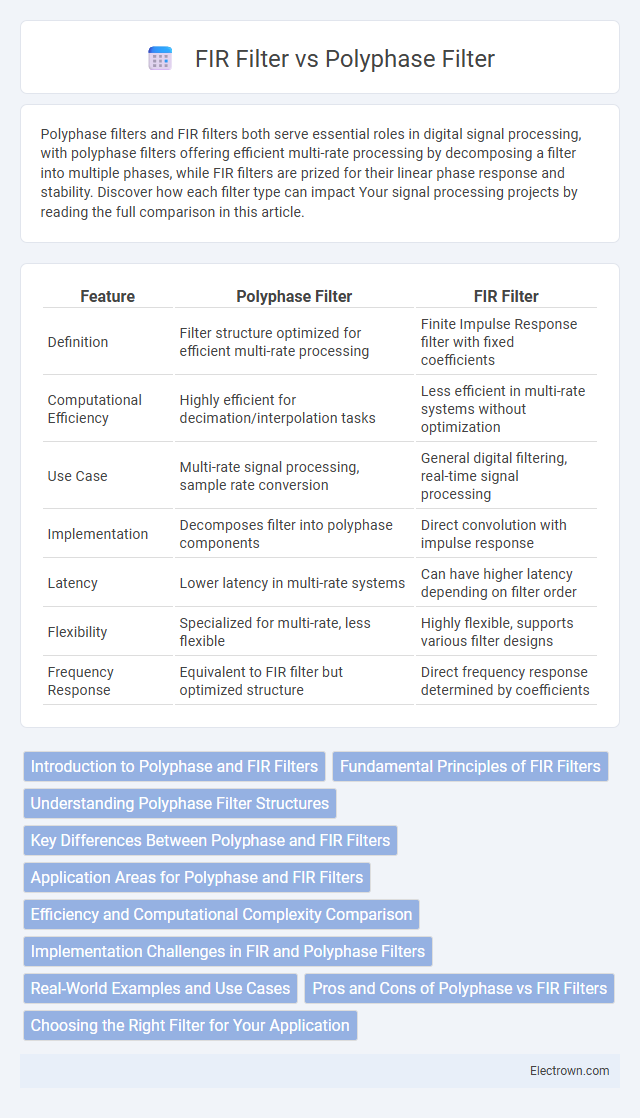
| Feature | Polyphase Filter | FIR Filter |
|---|---|---|
| Definition | Filter structure optimized for efficient multi-rate processing | Finite Impulse Response filter with fixed coefficients |
| Computational Efficiency | Highly efficient for decimation/interpolation tasks | Less efficient in multi-rate systems without optimization |
| Use Case | Multi-rate signal processing, sample rate conversion | General digital filtering, real-time signal processing |
| Implementation | Decomposes filter into polyphase components | Direct convolution with impulse response |
| Latency | Lower latency in multi-rate systems | Can have higher latency depending on filter order |
| Flexibility | Specialized for multi-rate, less flexible | Highly flexible, supports various filter designs |
| Frequency Response | Equivalent to FIR filter but optimized structure | Direct frequency response determined by coefficients |
Introduction to Polyphase and FIR Filters
Polyphase filters utilize multiple filter branches operating at different phases to enable efficient signal processing, especially in multirate systems, reducing computational complexity compared to traditional filtering methods. FIR (Finite Impulse Response) filters are linear time-invariant filters characterized by a finite-duration impulse response and are widely used for their inherent stability and linear phase properties. Polyphase implementations often optimize FIR filters by splitting them into sub-filters, enhancing performance in applications like decimation and interpolation.
Fundamental Principles of FIR Filters
FIR filters operate based on a finite impulse response characterized by a fixed number of coefficients determining the filter's output as a weighted sum of current and past input samples. The fundamental principle involves linear convolution, ensuring inherent stability and linear phase response, which is critical for signal integrity in applications like audio and communications. Polyphase filters optimize the implementation of FIR filters by decomposing the filter into multiple phases, improving computational efficiency in multirate processing without altering the underlying FIR filter principles.
Understanding Polyphase Filter Structures
Polyphase filter structures decompose a single Finite Impulse Response (FIR) filter into multiple sub-filters, optimizing multirate signal processing tasks such as interpolation and decimation. This approach significantly reduces computational complexity by enabling parallel processing of input data streams at different phases. Polyphase filters improve efficiency and reduce latency compared to conventional FIR filters, making them ideal for applications requiring real-time processing and resource-constrained environments.
Key Differences Between Polyphase and FIR Filters
Polyphase filters decompose a high-order FIR filter into multiple sub-filters operating at a lower rate, enabling efficient multirate signal processing and reduced computational complexity. FIR filters utilize a single, fixed set of coefficients applied directly to the input signal, offering linear phase response and inherent stability but potentially higher processing load for high-order designs. Polyphase structures excel in applications like sample rate conversion, while traditional FIR filters are preferred for straightforward filtering tasks requiring precise, non-subsampled operations.
Application Areas for Polyphase and FIR Filters
Polyphase filters are widely used in multirate signal processing applications such as sample rate conversion, decimation, and interpolation, where efficiency and reduced computational load are critical. FIR filters are preferred in applications requiring linear phase response and stability, including digital communication systems, audio processing, and control systems. Your choice depends on whether the primary need is efficient sample rate change (polyphase) or precise, linear-phase filtering characteristics (FIR).
Efficiency and Computational Complexity Comparison
Polyphase filters significantly enhance efficiency by decomposing a single high-rate FIR filter into multiple lower-rate sub-filters, reducing the number of multiplications and additions required per output sample. Compared to conventional FIR filters, polyphase structures leverage multirate processing to minimize computational complexity, especially in decimation and interpolation applications. This results in lower processing latency and power consumption, making polyphase filters ideal for real-time digital signal processing tasks.
Implementation Challenges in FIR and Polyphase Filters
Implementing FIR filters involves challenges such as increased computational complexity and higher power consumption due to the direct convolution of input signals with filter coefficients. Polyphase filters address these issues by decomposing the filter into multiple sub-filters that operate at lower sampling rates, simplifying hardware requirements and improving efficiency. Your design must balance the trade-offs between complexity and resource utilization, especially in real-time or power-constrained applications where polyphase filters can offer significant advantages.
Real-World Examples and Use Cases
Polyphase filters enhance FIR filter performance in applications like multirate signal processing, where they efficiently implement interpolation and decimation for software-defined radios and audio coding. FIR filters are widely used in equalizers and digital audio effects due to their linear phase characteristics and stability. Your choice depends on specific requirements such as computational efficiency in real-time systems versus filter precision in audio and communication devices.
Pros and Cons of Polyphase vs FIR Filters
Polyphase filters offer significant computational efficiency over standard FIR filters by decomposing the filtering process into multiple phases, reducing the number of required multiplications and making them ideal for multirate signal processing. FIR filters provide superior linear phase characteristics and are simpler to design and implement for fixed-rate signals but can be computationally intensive at high decimation or interpolation rates. Polyphase structures excel in applications requiring real-time processing and sample rate conversion but may introduce complexity in filter design compared to traditional FIR filters.
Choosing the Right Filter for Your Application
Polyphase filters offer efficient multirate signal processing by splitting the filtering operation into multiple phases, making them ideal for applications requiring decimation or interpolation with reduced computational load. FIR filters provide linear phase response and inherent stability, suitable for applications demanding precise control over frequency response and phase characteristics. Selecting between polyphase and FIR filters depends on the specific application needs, such as computational efficiency for real-time systems versus exact frequency and phase precision in filtering tasks.
Polyphase filter vs FIR filter Infographic
 electrown.com
electrown.com