Topological insulators feature insulating bulk states with conductive surface states protected by time-reversal symmetry, while Chern insulators exhibit quantized Hall conductance without an external magnetic field due to broken time-reversal symmetry and a nonzero Chern number. Discover how these fascinating materials differ in electronic properties and potential applications by reading the full article.
Table of Comparison
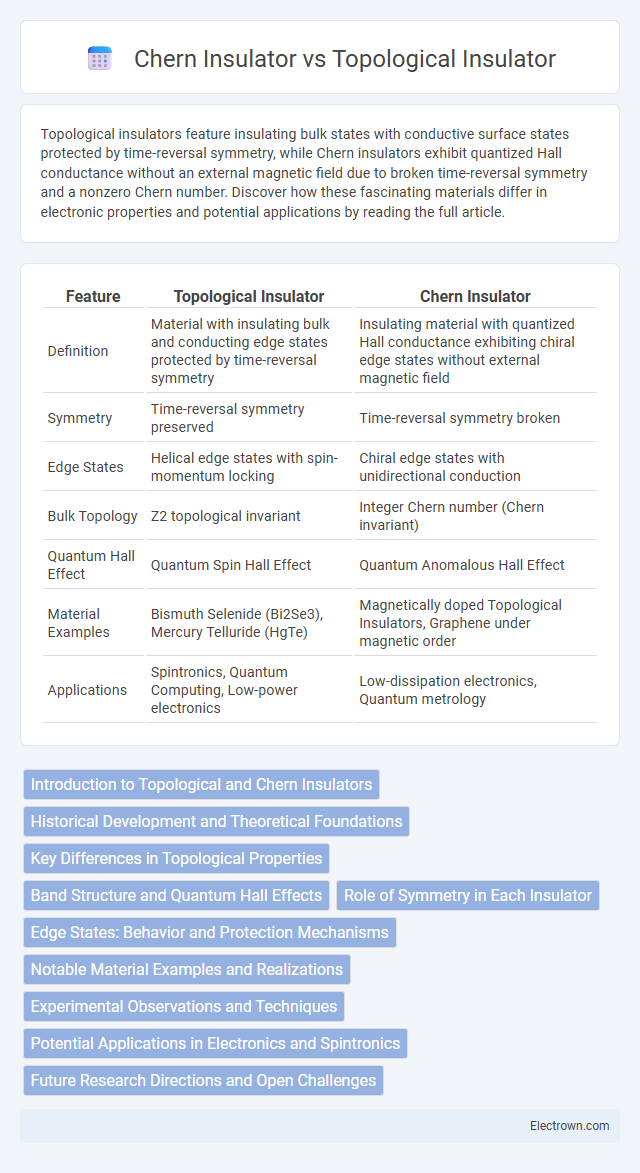
| Feature | Topological Insulator | Chern Insulator |
|---|---|---|
| Definition | Material with insulating bulk and conducting edge states protected by time-reversal symmetry | Insulating material with quantized Hall conductance exhibiting chiral edge states without external magnetic field |
| Symmetry | Time-reversal symmetry preserved | Time-reversal symmetry broken |
| Edge States | Helical edge states with spin-momentum locking | Chiral edge states with unidirectional conduction |
| Bulk Topology | Z2 topological invariant | Integer Chern number (Chern invariant) |
| Quantum Hall Effect | Quantum Spin Hall Effect | Quantum Anomalous Hall Effect |
| Material Examples | Bismuth Selenide (Bi2Se3), Mercury Telluride (HgTe) | Magnetically doped Topological Insulators, Graphene under magnetic order |
| Applications | Spintronics, Quantum Computing, Low-power electronics | Low-dissipation electronics, Quantum metrology |
Introduction to Topological and Chern Insulators
Topological insulators are materials with insulating interiors and conductive surface states protected by time-reversal symmetry, enabling robust edge conduction unaffected by impurities. Chern insulators, a subclass of topological phases, break time-reversal symmetry and exhibit quantized Hall conductance without an external magnetic field, characterized by a nonzero Chern number. Understanding these differences helps you explore their unique electronic properties and potential applications in spintronics and quantum computing.
Historical Development and Theoretical Foundations
Topological insulators emerged from the study of quantum spin Hall effects, with early theoretical foundations established by Kane and Mele in 2005, highlighting time-reversal symmetry-protected edge states. Chern insulators, also known as quantum anomalous Hall insulators, trace back to Haldane's 1988 model demonstrating a system with broken time-reversal symmetry supporting quantized Hall conductance without an external magnetic field. The theoretical framework for topological insulators relies on spin-orbit coupling and Z2 topological invariants, whereas Chern insulators are characterized by nonzero Chern numbers arising from broken time-reversal symmetry and band structure topology.
Key Differences in Topological Properties
Topological insulators exhibit time-reversal symmetry and are characterized by Z2 invariants, while Chern insulators break time-reversal symmetry and are defined by non-zero Chern numbers. The edge states in topological insulators are helical, with spin-momentum locking protecting against backscattering, whereas Chern insulators have chiral edge states that circulate unidirectionally due to an external magnetic field or magnetic ordering. Your understanding of these key differences is crucial for exploring applications in spintronics and quantum computing.
Band Structure and Quantum Hall Effects
Topological insulators exhibit a band structure characterized by an insulating bulk and conducting surface states protected by time-reversal symmetry, while Chern insulators display a gapped bulk with chiral edge states arising from nonzero Chern numbers without requiring an external magnetic field. The quantum Hall effect in topological insulators manifests as the quantum spin Hall effect with spin-polarized edge channels, whereas Chern insulators demonstrate the quantum anomalous Hall effect with quantized Hall conductance due to intrinsic magnetization. Understanding these distinctions in band topology and quantum Hall phenomena is crucial for your exploration of next-generation electronic and spintronic devices.
Role of Symmetry in Each Insulator
Topological insulators rely on time-reversal symmetry to protect their edge states, ensuring robust surface conductivity despite the insulating bulk. Chern insulators break time-reversal symmetry, typically due to magnetic ordering, leading to quantized Hall conductance without an external magnetic field. The presence or absence of specific symmetries defines the topological classification and electronic behavior unique to each insulator type.
Edge States: Behavior and Protection Mechanisms
Topological insulators feature edge states that are protected by time-reversal symmetry, preventing backscattering and ensuring robust conductance along edges even in the presence of non-magnetic impurities. Chern insulators exhibit chiral edge states characterized by unidirectional current flow, protected by a nonzero Chern number and broken time-reversal symmetry, which ensures dissipationless transport. Understanding these distinct protection mechanisms in your quantum device design can optimize edge state stability for potential applications in spintronics and quantum computing.
Notable Material Examples and Realizations
Bismuth selenide (Bi2Se3) and antimony telluride (Sb2Te3) are notable topological insulators exhibiting robust surface states protected by time-reversal symmetry. Chern insulators are exemplified by magnetically doped topological insulators such as chromium-doped (Bi,Sb)2Te3 and engineered two-dimensional materials like the Haldane model realized in cold atom systems. These material realizations demonstrate distinct topological phases characterized by time-reversal invariant surface conduction in topological insulators and quantized Hall conductance without an external magnetic field in Chern insulators.
Experimental Observations and Techniques
Experimental observations of topological insulators commonly involve angle-resolved photoemission spectroscopy (ARPES) to directly image surface states protected by time-reversal symmetry, while scanning tunneling microscopy (STM) reveals their robustness against non-magnetic impurities. In contrast, Chern insulators are characterized experimentally through transport measurements such as the quantum anomalous Hall effect, where quantized Hall conductance occurs without an external magnetic field, often detected using low-temperature magneto-transport setups. Your exploration of these materials relies heavily on advanced spectroscopic and transport techniques tailored to their distinct topological properties.
Potential Applications in Electronics and Spintronics
Topological insulators exhibit robust surface states that enable low-dissipation electronic transport, making them ideal for spintronic devices that exploit electron spin without energy loss. Chern insulators, characterized by quantized Hall conductance without external magnetic fields, are promising for developing fault-tolerant quantum computing and spin-based memory systems. Both materials advance the development of energy-efficient electronics with enhanced spin control and reduced power consumption.
Future Research Directions and Open Challenges
Future research on topological insulators and Chern insulators centers on realizing robust quantum computing applications by manipulating edge states and exploring non-Abelian anyons. Key challenges include material synthesis for high-temperature stability, controlling disorder effects, and integrating these insulators into scalable device architectures. Advancing your understanding of their topological phases could unlock new pathways in spintronics and fault-tolerant quantum information processing.
topological insulator vs Chern insulator Infographic
 electrown.com
electrown.com