Quantum logic gates manipulate qubits using principles of superposition and entanglement, enabling complex computations beyond the capabilities of classical logic gates, which operate on binary bits with fixed states of 0 or 1. Explore the rest of the article to understand how your computing tasks could be transformed by the advancements in quantum gate technology.
Table of Comparison
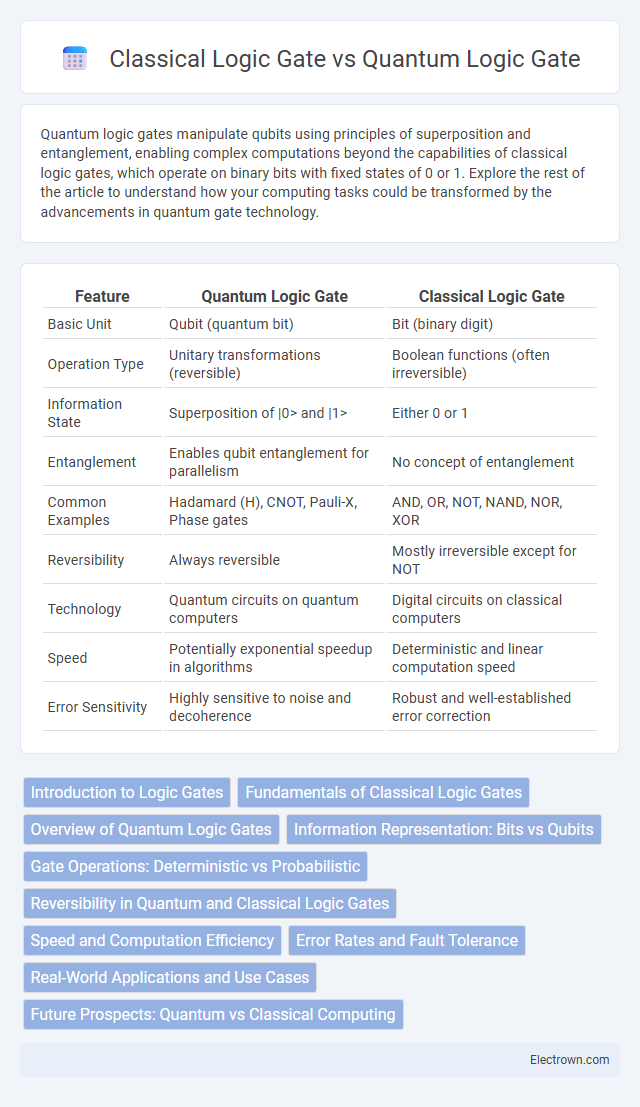
| Feature | Quantum Logic Gate | Classical Logic Gate |
|---|---|---|
| Basic Unit | Qubit (quantum bit) | Bit (binary digit) |
| Operation Type | Unitary transformations (reversible) | Boolean functions (often irreversible) |
| Information State | Superposition of |0> and |1> | Either 0 or 1 |
| Entanglement | Enables qubit entanglement for parallelism | No concept of entanglement |
| Common Examples | Hadamard (H), CNOT, Pauli-X, Phase gates | AND, OR, NOT, NAND, NOR, XOR |
| Reversibility | Always reversible | Mostly irreversible except for NOT |
| Technology | Quantum circuits on quantum computers | Digital circuits on classical computers |
| Speed | Potentially exponential speedup in algorithms | Deterministic and linear computation speed |
| Error Sensitivity | Highly sensitive to noise and decoherence | Robust and well-established error correction |
Introduction to Logic Gates
Quantum logic gates manipulate qubits using principles of superposition and entanglement, enabling complex quantum computations beyond classical capabilities. Classical logic gates process binary bits with deterministic operations like AND, OR, and NOT to perform Boolean algebra in digital circuits. Quantum gates operate through unitary transformations represented by matrices, whereas classical gates are based on fixed truth tables for binary inputs and outputs.
Fundamentals of Classical Logic Gates
Classical logic gates form the foundation of traditional digital circuits by performing basic Boolean operations like AND, OR, and NOT using binary inputs and outputs of 0s and 1s. These gates operate deterministically, processing one bit of information at a time based on fixed truth tables, enabling data manipulation in classical computers. Understanding these fundamentals is essential when comparing classical logic gates to quantum logic gates, which leverage qubits and quantum phenomena for parallel computation.
Overview of Quantum Logic Gates
Quantum logic gates manipulate qubits using principles of superposition and entanglement, enabling complex quantum computations beyond classical binary logic. Unlike classical logic gates that operate on bits with fixed states (0 or 1), quantum gates perform unitary transformations represented by matrices acting on quantum states. Examples include the Hadamard, Pauli-X, and CNOT gates, which facilitate quantum algorithms by creating and manipulating quantum coherence and correlations.
Information Representation: Bits vs Qubits
Classical logic gates process information using bits that exist strictly as 0 or 1, enabling binary operations essential for traditional computing. Quantum logic gates manipulate qubits, which exploit quantum phenomena such as superposition and entanglement, allowing for simultaneous representation of multiple states. Understanding this fundamental difference in information representation is crucial for leveraging your quantum computing capabilities effectively.
Gate Operations: Deterministic vs Probabilistic
Classical logic gates perform deterministic operations where inputs produce specific outputs based on Boolean algebra, ensuring predictable and repeatable results. Quantum logic gates manipulate qubits through unitary transformations, enabling probabilistic outcomes due to superposition and entanglement properties inherent in quantum states. The probabilistic nature of quantum gates allows for parallel processing and complex computations that classical deterministic gates cannot efficiently achieve.
Reversibility in Quantum and Classical Logic Gates
Quantum logic gates are inherently reversible, meaning each input state maps uniquely to an output state, allowing quantum computations to be undone without loss of information. Classical logic gates, such as AND, OR, and NAND, are generally irreversible because they can produce the same output from multiple inputs, causing information loss. Your understanding of reversibility highlights the advantage of quantum gates in error correction and energy-efficient computing.
Speed and Computation Efficiency
Quantum logic gates operate on qubits, enabling superposition and entanglement, which drastically increase computational speed and efficiency compared to classical logic gates that process binary bits sequentially. The parallelism inherent in quantum gates allows quantum algorithms like Shor's and Grover's to solve complex problems exponentially faster than classical circuits, reducing computation time for tasks such as factoring large numbers and database searching. This quantum advantage translates to higher throughput and lower resource consumption in quantum computing models, outperforming classical gates in handling intricate computational processes.
Error Rates and Fault Tolerance
Quantum logic gates exhibit significantly higher error rates compared to classical logic gates due to decoherence and quantum noise, necessitating advanced quantum error correction techniques. Classical gates benefit from well-established fault-tolerant designs and low error probabilities, with error rates typically below 10^-15 in modern CMOS technology. Fault tolerance in quantum computing relies on deploying entangled qubits and redundancy through error-correcting codes, whereas classical systems use scalable, deterministic logic circuits with straightforward error-checking mechanisms.
Real-World Applications and Use Cases
Quantum logic gates enable advanced computation in quantum computers, powering real-world applications such as cryptography, optimization problems, and material simulations. Classical logic gates remain foundational in everyday digital devices like smartphones, calculators, and embedded systems. Your ability to harness quantum gates enhances fields like secure communication and drug discovery, surpassing classical computational limits.
Future Prospects: Quantum vs Classical Computing
Quantum logic gates harness principles of superposition and entanglement, enabling quantum computers to perform complex calculations exponentially faster than classical logic gates, which operate on binary states. Future prospects for quantum computing include breakthroughs in cryptography, optimization problems, and drug discovery, outperforming classical computing's limitations. However, classical logic gates remain essential for traditional computing tasks and are expected to coexist with quantum processors in hybrid systems.
quantum logic gate vs classical logic gate Infographic
 electrown.com
electrown.com