Squeezed states exhibit reduced quantum noise in one variable at the expense of increased noise in its conjugate, enhancing precision beyond standard quantum limits, while coherent states maintain equal uncertainty in both variables, resembling classical harmonic oscillators. Discover how these quantum states differ and impact applications in advanced quantum technologies by reading the rest of the article.
Table of Comparison
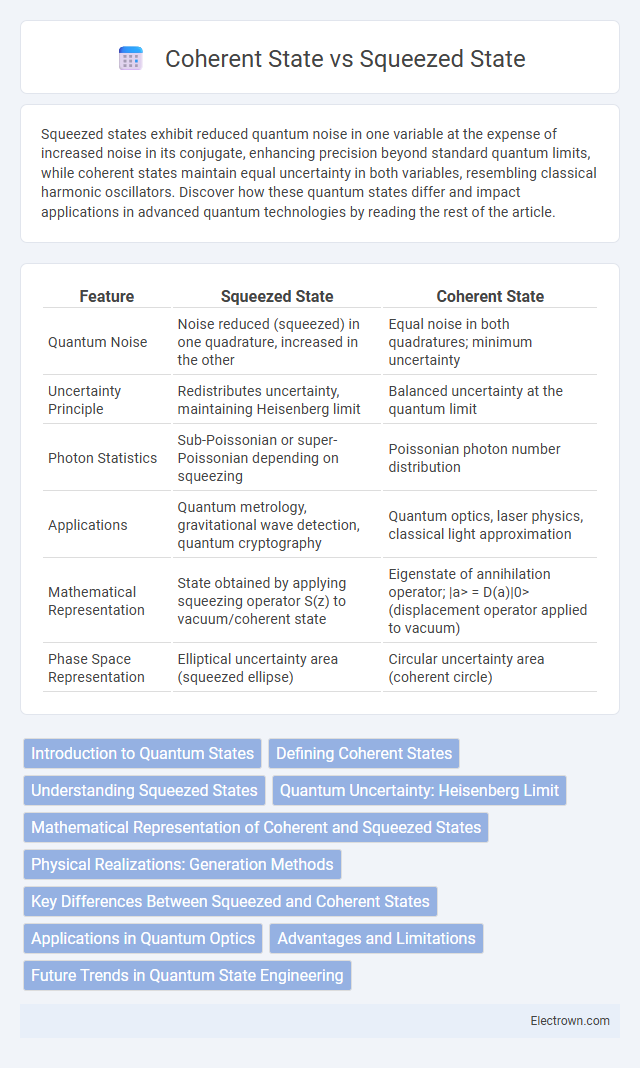
| Feature | Squeezed State | Coherent State |
|---|---|---|
| Quantum Noise | Noise reduced (squeezed) in one quadrature, increased in the other | Equal noise in both quadratures; minimum uncertainty |
| Uncertainty Principle | Redistributes uncertainty, maintaining Heisenberg limit | Balanced uncertainty at the quantum limit |
| Photon Statistics | Sub-Poissonian or super-Poissonian depending on squeezing | Poissonian photon number distribution |
| Applications | Quantum metrology, gravitational wave detection, quantum cryptography | Quantum optics, laser physics, classical light approximation |
| Mathematical Representation | State obtained by applying squeezing operator S(z) to vacuum/coherent state | Eigenstate of annihilation operator; |a> = D(a)|0> (displacement operator applied to vacuum) |
| Phase Space Representation | Elliptical uncertainty area (squeezed ellipse) | Circular uncertainty area (coherent circle) |
Introduction to Quantum States
Squeezed states and coherent states represent fundamental quantum states in quantum optics, with coherent states closely resembling classical light characterized by minimum uncertainty equally distributed between position and momentum quadratures. Squeezed states exhibit reduced quantum noise in one quadrature at the expense of increased noise in the conjugate quadrature, enabling measurements beyond the standard quantum limit. These states are essential for precision measurements, quantum information processing, and enhancing sensitivity in gravitational wave detectors.
Defining Coherent States
Coherent states represent quantum states of the electromagnetic field that closely resemble classical oscillations, characterized by minimum uncertainty with equal variance in both quadratures. Defined as eigenstates of the annihilation operator, coherent states maintain their shape during time evolution, making them essential in quantum optics and communication. These states exhibit a Poissonian photon number distribution and serve as a benchmark for comparing nonclassical states like squeezed states.
Understanding Squeezed States
Squeezed states represent quantum states where the uncertainty in one quadrature component is reduced below the standard quantum limit, enhancing precision beyond coherent states, which maintain equal uncertainty in both quadratures. These states are fundamental in quantum optics and metrology, enabling improvements in measurements like gravitational wave detection through noise reduction in a specific quadrature. The generation of squeezed states typically involves nonlinear optical processes such as parametric down-conversion in nonlinear crystals, creating correlations that redistribute quantum noise asymmetrically.
Quantum Uncertainty: Heisenberg Limit
Squeezed states reduce quantum uncertainty in one observable below the Heisenberg limit while increasing uncertainty in the conjugate variable, unlike coherent states that maintain equal uncertainty at the standard quantum limit. Your measurements using squeezed states can surpass the precision of coherent states in applications such as gravitational wave detection or quantum metrology. These states optimize quantum uncertainty, approaching the fundamental limits set by the Heisenberg uncertainty principle.
Mathematical Representation of Coherent and Squeezed States
Coherent states |a> are eigenstates of the annihilation operator a, represented as |a> = D(a)|0> , where D(a) = exp(aa+ - a*a) is the displacement operator acting on the vacuum state |0> . Squeezed states |x> are generated by applying the squeezing operator S(x) = exp( 1/2(x*a2 - xa+2)) to the vacuum, where the complex parameter x = r e^{ith} defines the squeezing magnitude r and angle th. The mathematical distinction arises because coherent states preserve minimum uncertainty with symmetric quadrature variance, while squeezed states redistribute uncertainty by reducing variance in one quadrature below the standard quantum limit at the expense of increased variance in the conjugate quadrature.
Physical Realizations: Generation Methods
Physical realizations of squeezed states typically involve nonlinear optical processes such as parametric down-conversion in nonlinear crystals and four-wave mixing in atomic vapors, which reduce quantum noise in one quadrature below the standard quantum limit. Coherent states are commonly generated by stable single-mode lasers providing a well-defined amplitude and phase with minimum uncertainty in both quadratures. Advanced techniques for squeezed state generation include optical parametric oscillators and fiber-based squeezing, while coherent states rely mainly on direct laser emission with minimal external modulation.
Key Differences Between Squeezed and Coherent States
Squeezed states exhibit reduced quantum uncertainty in one quadrature at the expense of increased uncertainty in the conjugate quadrature, whereas coherent states maintain equal quantum uncertainty in both quadratures, representing minimum uncertainty states with classical-like properties. Coherent states resemble classical electromagnetic waves with Poissonian photon number statistics, while squeezed states have non-classical photon statistics that improve precision in quantum measurements. These fundamental differences impact applications: coherent states dominate in classical communication, while squeezed states enhance sensitivity in quantum metrology and quantum information processing.
Applications in Quantum Optics
Squeezed states improve precision measurements by reducing quantum noise below the standard quantum limit, making them essential for applications like gravitational wave detection and quantum metrology. Coherent states, characterized by minimum uncertainty and classical-like behavior, serve as fundamental resources in quantum communication and laser physics. Your ability to manipulate these states enhances the performance of quantum sensors and secure information transfer systems.
Advantages and Limitations
Squeezed states offer reduced quantum noise in one quadrature, enhancing precision in measurements such as gravitational wave detection, but their generation and stabilization require complex apparatus and remain sensitive to losses. Coherent states resemble classical light with balanced noise distribution, providing robustness and ease of generation while limiting sensitivity improvements in quantum sensing. Understanding these trade-offs is crucial for optimizing Your quantum optics applications.
Future Trends in Quantum State Engineering
Future trends in quantum state engineering emphasize the development of advanced squeezed states to enhance precision measurements beyond the standard quantum limit, crucial for applications in quantum metrology and gravitational wave detection. Coherent states remain foundational for quantum communication and computing, but integrating squeezed states into these platforms promises improved noise reduction and error correction. Your ability to harness both states will drive innovations in scalable quantum technologies and hybrid quantum systems.
squeezed state vs coherent state Infographic
 electrown.com
electrown.com