Density matrices provide a comprehensive description of quantum states, capturing both pure states and mixed states, unlike wavefunctions which represent only pure states. For a deeper understanding of how these formalisms impact quantum measurements and computations, read the rest of the article.
Table of Comparison
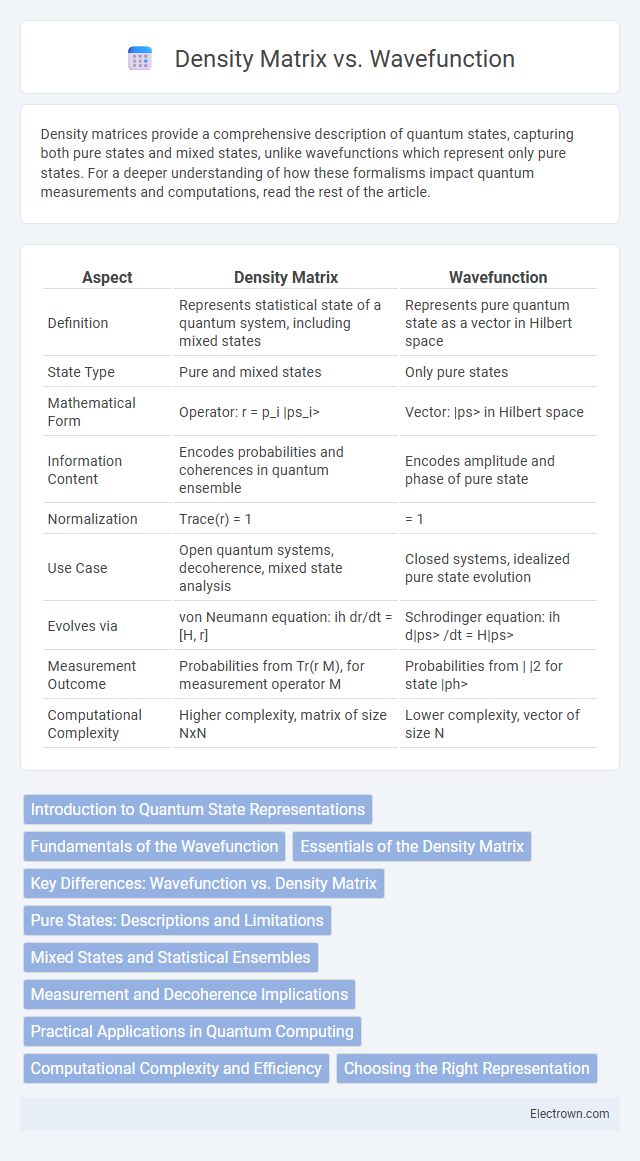
| Aspect | Density Matrix | Wavefunction |
|---|---|---|
| Definition | Represents statistical state of a quantum system, including mixed states | Represents pure quantum state as a vector in Hilbert space |
| State Type | Pure and mixed states | Only pure states |
| Mathematical Form | Operator: r = p_i |ps_i> | Vector: |ps> in Hilbert space |
|
| Information Content | Encodes probabilities and coherences in quantum ensemble | Encodes amplitude and phase of pure state |
| Normalization | Trace(r) = 1 | |
| Use Case | Open quantum systems, decoherence, mixed state analysis | Closed systems, idealized pure state evolution |
| Evolves via | von Neumann equation: ih dr/dt = [H, r] | Schrodinger equation: ih d|ps> /dt = H|ps> |
| Measurement Outcome | Probabilities from Tr(r M), for measurement operator M | Probabilities from | |
| Computational Complexity | Higher complexity, matrix of size NxN | Lower complexity, vector of size N |
Introduction to Quantum State Representations
Quantum state representations include the wavefunction and the density matrix, each providing distinct insights into quantum systems. The wavefunction offers a complete description of a pure quantum state with complex probability amplitudes, essential for predicting measurement outcomes. The density matrix extends this by representing both pure and mixed states, capturing statistical mixtures and coherence, making it crucial for understanding open quantum systems and decoherence effects in your quantum analyses.
Fundamentals of the Wavefunction
The wavefunction is a fundamental concept in quantum mechanics representing the quantum state of a system, described by a complex-valued function that encodes probabilities of measurable outcomes. Unlike the density matrix, which generalizes to mixed states and statistical ensembles, the wavefunction typically describes pure states with full information about coherence and phase relations. It evolves according to the Schrodinger equation, providing a complete description of quantum interference and superposition phenomena fundamental to quantum behavior.
Essentials of the Density Matrix
The density matrix provides a comprehensive description of a quantum system's statistical state, capturing both pure states and mixed states, unlike the wavefunction which represents only pure states. It encodes probabilities and coherences between quantum states, allowing for the calculation of expectation values and observables without referencing a specific basis. Essential properties include being Hermitian, positive semidefinite, and having a unit trace, ensuring physically meaningful probability distributions in quantum mechanics.
Key Differences: Wavefunction vs. Density Matrix
Wavefunctions represent quantum states as complex probability amplitudes, providing complete information about pure states but failing to describe mixed states or statistical ensembles. Density matrices generalize this by encoding both pure and mixed states, capturing probabilistic mixtures and coherence, which wavefunctions cannot represent alone. Your understanding of quantum systems improves by using density matrices for open systems or measurements involving decoherence, where wavefunctions are insufficient.
Pure States: Descriptions and Limitations
Pure states in quantum mechanics are typically represented by wavefunctions, providing a complete description of a quantum system's state with maximum knowledge and coherence. The density matrix formalism, while capable of representing pure states as projection operators, extends beyond wavefunctions by describing statistical mixtures and partial information scenarios. Your choice between these formalisms depends on whether the system is in a well-defined pure state or a complex mixture requiring probabilistic treatment.
Mixed States and Statistical Ensembles
The density matrix efficiently represents mixed states and statistical ensembles by encoding probabilities of various quantum states, unlike the wavefunction, which describes a pure state. Mixed states arise when a quantum system exists as a probabilistic combination of multiple pure states, making the density matrix essential for capturing this statistical nature. Your analysis of quantum systems involving decoherence or incomplete knowledge relies heavily on density matrices for accurate and comprehensive descriptions.
Measurement and Decoherence Implications
Density matrices provide a comprehensive framework for describing quantum systems, capturing both pure states and mixed states that arise from decoherence, unlike wavefunctions which represent only pure states. Measurement outcomes are probabilistically encoded in density matrices, allowing for the description of statistical mixtures resulting from interactions with the environment, crucial for understanding quantum decoherence. Your analysis of quantum measurement processes benefits from using density matrices, as they accurately model the loss of coherence and the complex dynamics involved in realistic quantum systems.
Practical Applications in Quantum Computing
Density matrices provide a versatile framework for representing mixed quantum states, essential for practical quantum computing tasks involving noise and decoherence. Unlike wavefunctions, which describe pure states, density matrices capture statistical mixtures and enable error correction, quantum state tomography, and efficient simulation of open quantum systems. Mastery of density matrix formalism enhances your ability to implement robust quantum algorithms and optimize performance in real-world quantum devices.
Computational Complexity and Efficiency
Density matrices provide a more computationally efficient framework for simulating mixed quantum states compared to wavefunctions, especially in systems with decoherence or entanglement. While wavefunctions require exponential memory scaling with the number of particles, density matrices allow for partial system descriptions, reducing complexity in certain cases. Your choice between density matrix and wavefunction approaches depends on the balance between computational resources and the need for representing pure versus mixed states accurately.
Choosing the Right Representation
Density matrices offer a versatile framework for representing mixed quantum states, capturing statistical ensembles and decoherence effects that pure wavefunctions cannot. Wavefunctions provide a concise description of pure states with maximal information but lack the capability to represent classical uncertainty or partial quantum states. Selecting between a density matrix and wavefunction depends on whether the system involves pure states or statistical mixtures, with density matrices preferred for open quantum systems and entangled environments.
density matrix vs wavefunction Infographic
 electrown.com
electrown.com