The Hong-Ou-Mandel effect demonstrates two-photon interference resulting in photon bunching at a beam splitter, revealing fundamental quantum properties of identical photons, while the Hanbury Brown-Twiss effect measures intensity correlations that highlight photon statistics and coherence in classical or quantum light sources. Explore the rest of the article to understand how these phenomena differentiate your insights into quantum optics experiments.
Table of Comparison
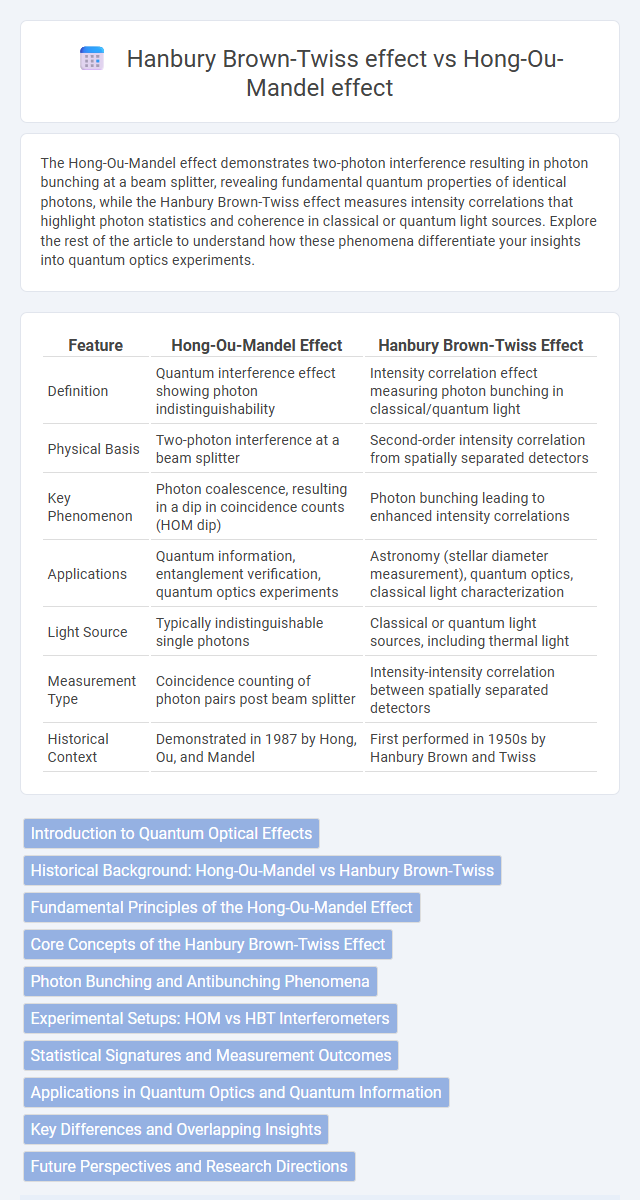
| Feature | Hong-Ou-Mandel Effect | Hanbury Brown-Twiss Effect |
|---|---|---|
| Definition | Quantum interference effect showing photon indistinguishability | Intensity correlation effect measuring photon bunching in classical/quantum light |
| Physical Basis | Two-photon interference at a beam splitter | Second-order intensity correlation from spatially separated detectors |
| Key Phenomenon | Photon coalescence, resulting in a dip in coincidence counts (HOM dip) | Photon bunching leading to enhanced intensity correlations |
| Applications | Quantum information, entanglement verification, quantum optics experiments | Astronomy (stellar diameter measurement), quantum optics, classical light characterization |
| Light Source | Typically indistinguishable single photons | Classical or quantum light sources, including thermal light |
| Measurement Type | Coincidence counting of photon pairs post beam splitter | Intensity-intensity correlation between spatially separated detectors |
| Historical Context | Demonstrated in 1987 by Hong, Ou, and Mandel | First performed in 1950s by Hanbury Brown and Twiss |
Introduction to Quantum Optical Effects
The Hong-Ou-Mandel effect demonstrates quantum interference where two indistinguishable photons arriving simultaneously at a beam splitter exit together, revealing the non-classical nature of light. The Hanbury Brown-Twiss effect measures intensity correlations of photons from a light source, used to determine spatial coherence and photon statistics, highlighting classical versus quantum light behavior. Understanding these quantum optical effects helps you analyze photon interactions and coherence properties crucial in quantum communication and photonic technologies.
Historical Background: Hong-Ou-Mandel vs Hanbury Brown-Twiss
The Hong-Ou-Mandel effect, discovered in 1987, demonstrated quantum interference between two indistinguishable photons leading to photon bunching at a beam splitter, revolutionizing the understanding of quantum entanglement and photon indistinguishability. In contrast, the Hanbury Brown-Twiss effect, first observed in the 1950s, used intensity correlations from light sources to measure stellar sizes, laying foundational work for quantum optics and photon correlation techniques. Your grasp of these effects highlights the progression from classical photon correlation to quantum interference phenomena in photonics research.
Fundamental Principles of the Hong-Ou-Mandel Effect
The Hong-Ou-Mandel effect arises from the quantum interference of two indistinguishable photons entering a beam splitter simultaneously, resulting in both photons exiting together through the same output port. This phenomenon is fundamentally rooted in the bosonic nature of photons and their indistinguishability, leading to a characteristic dip in coincidence detection rates known as the Hong-Ou-Mandel dip. Understanding this effect is crucial for applications in quantum optics and quantum information, where controlling photon interference is essential for achieving high-fidelity operations.
Core Concepts of the Hanbury Brown-Twiss Effect
The Hanbury Brown-Twiss effect demonstrates photon bunching through intensity interferometry, revealing correlations in photon arrival times at separate detectors. It relies on measuring second-order coherence, highlighting the statistical nature of light and enabling determinations of source size and structure in astrophysics. This effect contrasts with the Hong-Ou-Mandel effect, which involves two-photon interference at a beamsplitter leading to photon coalescence rather than intensity correlations.
Photon Bunching and Antibunching Phenomena
The Hong-Ou-Mandel effect demonstrates photon antibunching through quantum interference, where identical photons entering a beam splitter exit together in the same output mode, creating a dip in coincidence counts known as the HOM dip. In contrast, the Hanbury Brown-Twiss effect reveals classical photon bunching by measuring intensity correlations from a thermal light source, showing increased coincidence rates due to photon clustering. These phenomena highlight fundamental quantum and classical differences in photon correlation behavior, with the HOM effect underpinning quantum entanglement applications and HBT informing astronomical intensity interferometry.
Experimental Setups: HOM vs HBT Interferometers
The Hong-Ou-Mandel (HOM) effect employs a beam splitter where two indistinguishable photons enter separate input ports and interfere, resulting in photon bunching detected by coincident photodetectors at the output arms. The Hanbury Brown-Twiss (HBT) interferometer uses a beam splitter to split light from a single source to measure intensity correlations between two detectors, focusing on second-order coherence without requiring indistinguishable photons. HOM interferometers require entangled or identical photons for two-photon interference, while HBT setups analyze statistical photon arrival times to determine spatial or temporal coherence properties of classical or quantum light sources.
Statistical Signatures and Measurement Outcomes
The Hong-Ou-Mandel effect exhibits photon bunching characterized by a dip in coincidence counts due to two indistinguishable photons interfering on a beamsplitter, revealing quantum statistical properties. The Hanbury Brown-Twiss effect measures intensity correlations and demonstrates bunching behavior for thermal light sources through photon statistical fluctuations in classical or quantum fields. Measurement outcomes in the Hong-Ou-Mandel experiment highlight quantum indistinguishability and entanglement, whereas the Hanbury Brown-Twiss experiment primarily reveals second-order coherence and intensity correlation statistics.
Applications in Quantum Optics and Quantum Information
The Hong-Ou-Mandel effect is crucial for quantum optics applications such as entanglement generation, quantum teleportation, and photonic quantum computing due to its ability to reveal photon indistinguishability and interference. The Hanbury Brown-Twiss effect finds use in quantum optics by measuring photon correlations and characterizing light sources, enabling quantum imaging and precise photon counting. Understanding these effects enhances your ability to manipulate quantum states for advances in quantum information processing and communication technologies.
Key Differences and Overlapping Insights
The Hong-Ou-Mandel effect demonstrates quantum interference by showing photon indistinguishability through a dip in coincident detection rates, whereas the Hanbury Brown-Twiss effect measures intensity correlations to reveal photon bunching or anti-bunching in classical and quantum light sources. Both effects provide insights into photon statistics and coherence properties, with the Hong-Ou-Mandel effect emphasizing two-photon interference and the Hanbury Brown-Twiss effect characterizing temporal correlations. Your understanding of quantum optics improves by exploring how these phenomena collectively inform studies on particle indistinguishability and light source coherence.
Future Perspectives and Research Directions
Research into the Hong-Ou-Mandel (HOM) effect is advancing toward integrating quantum photonics with scalable quantum computing and secure quantum communication, leveraging its photon indistinguishability for enhanced entanglement generation. Future studies on the Hanbury Brown-Twiss (HBT) effect aim to refine quantum imaging and photon correlation methods, expanding applications in astrophysics and fundamental quantum optics. Your understanding of these quantum interference phenomena can aid in developing novel photonic devices that harness quantum correlations for next-generation technologies.
Hong-Ou-Mandel effect vs Hanbury Brown-Twiss effect Infographic
 electrown.com
electrown.com