Photon polarization describes the orientation of the electromagnetic wave's oscillations, while electron spin represents a quantum property related to its intrinsic angular momentum. Understanding these differences can enhance your grasp of quantum mechanics; explore the rest of the article to learn more.
Table of Comparison
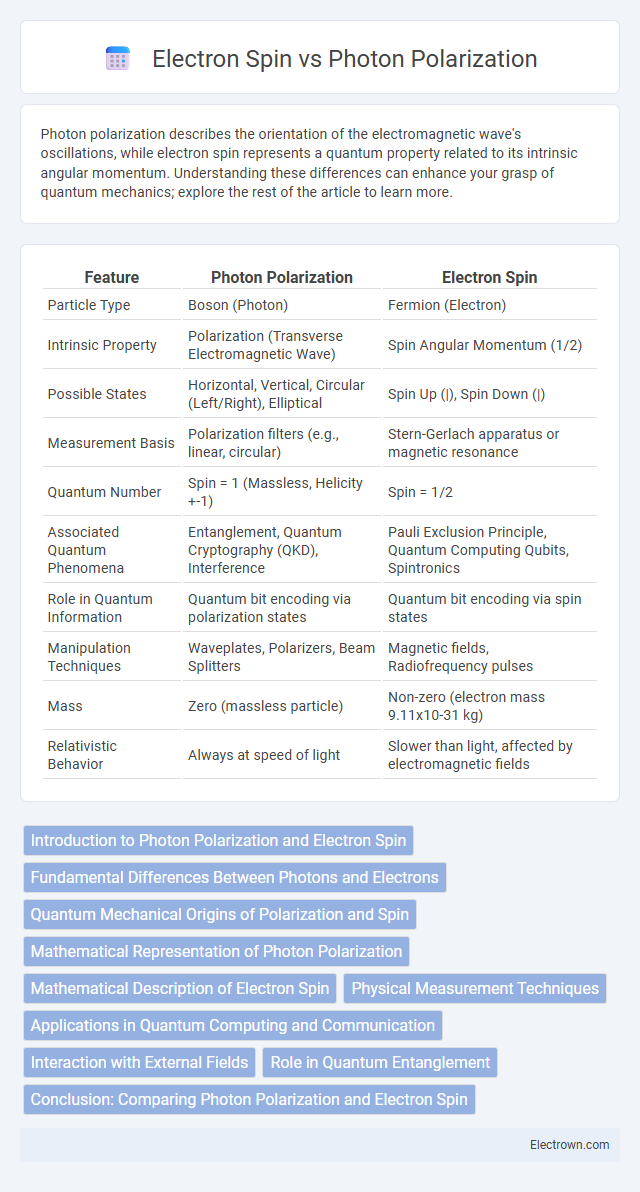
| Feature | Photon Polarization | Electron Spin |
|---|---|---|
| Particle Type | Boson (Photon) | Fermion (Electron) |
| Intrinsic Property | Polarization (Transverse Electromagnetic Wave) | Spin Angular Momentum (1/2) |
| Possible States | Horizontal, Vertical, Circular (Left/Right), Elliptical | Spin Up (|), Spin Down (|) |
| Measurement Basis | Polarization filters (e.g., linear, circular) | Stern-Gerlach apparatus or magnetic resonance |
| Quantum Number | Spin = 1 (Massless, Helicity +-1) | Spin = 1/2 |
| Associated Quantum Phenomena | Entanglement, Quantum Cryptography (QKD), Interference | Pauli Exclusion Principle, Quantum Computing Qubits, Spintronics |
| Role in Quantum Information | Quantum bit encoding via polarization states | Quantum bit encoding via spin states |
| Manipulation Techniques | Waveplates, Polarizers, Beam Splitters | Magnetic fields, Radiofrequency pulses |
| Mass | Zero (massless particle) | Non-zero (electron mass 9.11x10-31 kg) |
| Relativistic Behavior | Always at speed of light | Slower than light, affected by electromagnetic fields |
Introduction to Photon Polarization and Electron Spin
Photon polarization describes the orientation of the electromagnetic wave's oscillations, characterized by linear, circular, or elliptical states that define how light interacts with materials and devices like polarizers. Electron spin, a fundamental quantum property, represents an intrinsic form of angular momentum with two possible states--spin-up and spin-down--that are crucial for magnetic behavior and quantum computing applications. Understanding these distinct yet fundamental quantum characteristics enables you to manipulate light and matter at the quantum level for advanced technological developments.
Fundamental Differences Between Photons and Electrons
Photons exhibit polarization, a property linked to their transverse electromagnetic wave nature and absence of rest mass, allowing states such as linear, circular, and elliptical polarization. Electrons possess intrinsic spin, a quantum mechanical property representing angular momentum with discrete values of +- 1/2, reflecting their fermionic nature and mass. These fundamental differences arise from photons being massless bosons with spin-1 and electrons being massive fermions with spin- 1/2, resulting in distinct quantum behaviors and interaction mechanisms.
Quantum Mechanical Origins of Polarization and Spin
Photon polarization arises from the quantum mechanical property of photons as spin-1 bosons, described by the transverse nature of their electromagnetic fields and characterized by two orthogonal polarization states. Electron spin originates from intrinsic angular momentum, a fundamental quantum property of spin-1/2 fermions, described by Pauli spin matrices and underlying the electron's magnetic moment and quantum statistics. Both photon polarization and electron spin emerge from underlying quantum field theories, with polarization linked to the gauge symmetry of the electromagnetic field and spin arising from the representation theory of the Poincare group in relativistic quantum mechanics.
Mathematical Representation of Photon Polarization
Photon polarization is mathematically represented using Jones vectors or Stokes parameters, which describe the electric field oscillation directions in a complex vector space. Unlike electron spin, represented by spinors and Pauli matrices in a two-dimensional Hilbert space, photon polarization states form a two-dimensional vector space corresponding to horizontal and vertical polarization basis. Your understanding of photon polarization benefits from recognizing these linear algebra frameworks that distinguish it from quantum spin descriptions.
Mathematical Description of Electron Spin
Electron spin is mathematically described using Pauli matrices and spinors in a two-dimensional complex Hilbert space, representing the intrinsic angular momentum and corresponding quantum states. The spin operators satisfy the SU(2) Lie algebra commutation relations, with eigenvalues of +-h/2 defining the spin-up and spin-down states along a chosen axis. Unlike photon polarization, which is described by two-dimensional Jones vectors in a Hilbert space representing transverse electric field components, electron spin requires a more fundamental algebraic structure to capture its quantum mechanical properties accurately.
Physical Measurement Techniques
Photon polarization is measured using polarizers, wave plates, and photodetectors to analyze the orientation of the electromagnetic wave's oscillations. Electron spin is detected through techniques like Stern-Gerlach experiments, which use non-uniform magnetic fields to spatially separate spin states, and spin-resonance methods such as Electron Spin Resonance (ESR) spectroscopy. Your choice of measurement technique depends on the particle type and desired precision in characterizing quantum spin or polarization states.
Applications in Quantum Computing and Communication
Photon polarization enables high-speed quantum communication through entangled photon states, providing secure data transmission in quantum key distribution protocols. Electron spin offers a robust platform for quantum computing via spin qubits, allowing scalable quantum information processing with long coherence times in solid-state systems. Combining photon polarization and electron spin techniques enhances hybrid quantum networks, facilitating efficient quantum state transfer and error correction in advanced quantum technologies.
Interaction with External Fields
Photon polarization interacts with external electromagnetic fields primarily through changes in the propagation medium, such as birefringence or Faraday rotation, altering the polarization state without direct coupling to magnetic fields. Electron spin directly couples to external magnetic fields via the Zeeman effect, causing energy level splitting and spin precession that can be precisely controlled with magnetic resonance techniques. Understanding these interactions allows you to manipulate photon polarization for optical communication and electron spin for quantum computing applications.
Role in Quantum Entanglement
Photon polarization and electron spin serve as fundamental quantum properties enabling quantum entanglement, where paired particles exhibit correlated states regardless of distance. Photon polarization states, represented as horizontal, vertical, or superpositions, facilitate entanglement via Bell states crucial for quantum communication protocols. Electron spin, characterized by its intrinsic angular momentum with spin-up or spin-down states, underpins entanglement in quantum computing and spintronics, allowing manipulation of qubit states for information processing.
Conclusion: Comparing Photon Polarization and Electron Spin
Photon polarization and electron spin are fundamental quantum properties governing particle behavior, with polarization describing the orientation of oscillating electric fields in photons, while spin represents an intrinsic form of angular momentum in electrons. Photon polarization states can be manipulated using optical devices like polarizers, enabling applications in quantum communication, whereas electron spin is pivotal in spintronics and quantum computing due to its magnetic moment and coupling with magnetic fields. Both phenomena demonstrate quantum superposition and entanglement, but electron spin involves fermionic particles with half-integer spin, contrasting with the bosonic nature and integer spin of photons, leading to distinct physical behaviors and technological uses.
photon polarization vs electron spin Infographic
 electrown.com
electrown.com