A quantum oscillator describes a system where energy levels are quantized, exhibiting discrete states and uncertainties governed by quantum mechanics, unlike the classical harmonic oscillator which follows continuous sinusoidal motion determined by classical physics. Explore how these fundamental concepts differ and their implications in physics by reading the full article.
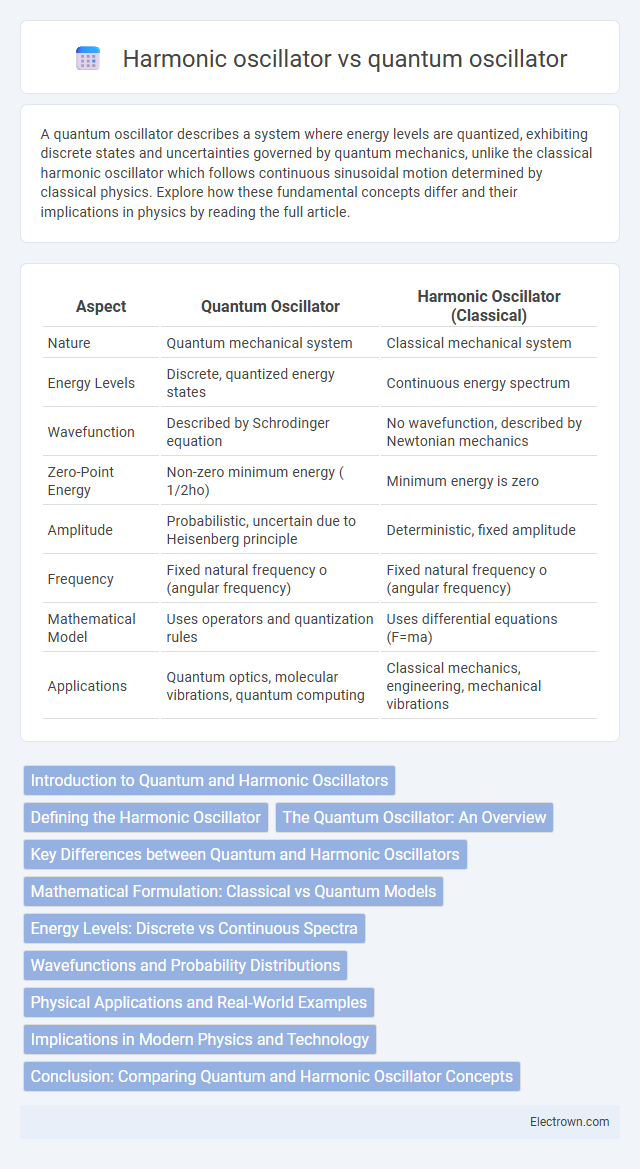
Table of Comparison
| Aspect | Quantum Oscillator | Harmonic Oscillator (Classical) |
|---|---|---|
| Nature | Quantum mechanical system | Classical mechanical system |
| Energy Levels | Discrete, quantized energy states | Continuous energy spectrum |
| Wavefunction | Described by Schrodinger equation | No wavefunction, described by Newtonian mechanics |
| Zero-Point Energy | Non-zero minimum energy ( 1/2ho) | Minimum energy is zero |
| Amplitude | Probabilistic, uncertain due to Heisenberg principle | Deterministic, fixed amplitude |
| Frequency | Fixed natural frequency o (angular frequency) | Fixed natural frequency o (angular frequency) |
| Mathematical Model | Uses operators and quantization rules | Uses differential equations (F=ma) |
| Applications | Quantum optics, molecular vibrations, quantum computing | Classical mechanics, engineering, mechanical vibrations |
Introduction to Quantum and Harmonic Oscillators
Quantum oscillators describe systems where energy levels are quantized, differing fundamentally from classical harmonic oscillators that assume continuous energy variation. In quantum mechanics, the quantum oscillator is modeled using wavefunctions and operators, capturing phenomena like zero-point energy absent in classical harmonic oscillators. Understanding these oscillators enables you to analyze molecular vibrations, quantum field modes, and nanoscale physical systems with precision.
Defining the Harmonic Oscillator
The harmonic oscillator is defined by a system where the restoring force is directly proportional to the displacement and acts in the opposite direction, often modeled by Hooke's law as F = -kx. In classical mechanics, this results in sinusoidal oscillations with a well-defined frequency determined by mass and spring constant. The quantum oscillator, a quantized version of this system, exhibits discrete energy levels described by the Schrodinger equation, with energy eigenvalues quantized as E_n = (n + 1/2)ho.
The Quantum Oscillator: An Overview
The quantum oscillator describes a system where energy levels are quantized, contrasting the continuous energy spectrum of the classical harmonic oscillator. It is governed by the Schrodinger equation, leading to discrete energy eigenstates characterized by quantum numbers. This quantum model is fundamental in understanding molecular vibrations, quantum field theory, and the behavior of particles in potential wells.
Key Differences between Quantum and Harmonic Oscillators
Quantum oscillators exhibit discrete energy levels governed by quantum mechanics, whereas classical harmonic oscillators possess continuous energy values described by classical physics. Quantum oscillators follow wavefunction properties and uncertainty principles, leading to probabilistic position and momentum, while harmonic oscillators have deterministic trajectories. The quantization of energy in quantum oscillators results in phenomena such as zero-point energy, absent in classical harmonic oscillators.
Mathematical Formulation: Classical vs Quantum Models
The harmonic oscillator in classical mechanics is described by a second-order differential equation \( m \frac{d^2x}{dt^2} + kx = 0 \), where \( m \) is mass and \( k \) is the spring constant, leading to sinusoidal motion solutions. The quantum oscillator employs the Schrodinger equation with the Hamiltonian operator \( \hat{H} = \frac{\hat{p}^2}{2m} + \frac{1}{2} k \hat{x}^2 \), quantizing energy levels into discrete eigenstates characterized by quantum numbers \( n \). Unlike the continuous energy spectrum of the classical system, the quantum harmonic oscillator exhibits quantized energy eigenvalues \( E_n = \hbar \omega \left(n + \frac{1}{2}\right) \), reflecting the fundamental difference in mathematical formulations.
Energy Levels: Discrete vs Continuous Spectra
Quantum oscillators exhibit discrete energy levels quantized according to Planck's constant, resulting in distinct, non-overlapping spectral lines. In contrast, classical harmonic oscillators possess a continuous energy spectrum, allowing any value within a range due to the absence of quantization. Understanding the discrete energy states of a quantum oscillator is essential for analyzing phenomena like atomic vibrations and photon emissions in your studies.
Wavefunctions and Probability Distributions
Quantum oscillators exhibit wavefunctions characterized by discrete energy eigenstates, described mathematically by Hermite polynomials multiplied by Gaussian envelopes. Probability distributions derived from these wavefunctions show quantized positional probabilities, featuring nodes where the probability density drops to zero. In contrast, classical harmonic oscillators lack wavefunctions and instead have continuous probability distributions governed by phase space trajectories.
Physical Applications and Real-World Examples
Quantum oscillators model particles in potential wells with discrete energy levels, critical in quantum mechanics for systems like vibrational modes in molecules and fields in quantum optics. Harmonic oscillators describe classic systems such as springs and pendulums, used in engineering for mechanical vibrations and electrical circuits. Understanding both models helps you analyze phenomena from nanoscale quantum dots to macroscopic oscillating systems.
Implications in Modern Physics and Technology
Quantum oscillators underpin the foundation of quantum mechanics by describing particles in discrete energy states, influencing advancements in quantum computing and quantum cryptography. Harmonic oscillators serve as idealized models for various physical systems, enabling precise predictions in classical mechanics and engineering applications such as signal processing and vibration analysis. The interplay between quantum and harmonic oscillators drives innovations in nanotechnology and quantum sensors, enhancing the sensitivity and performance of modern measurement devices.
Conclusion: Comparing Quantum and Harmonic Oscillator Concepts
Quantum oscillators exhibit discrete energy levels and probabilistic behavior governed by wavefunctions, contrasting with harmonic oscillators' continuous energy spectrum and classical deterministic motion. The quantum model incorporates uncertainty principles and zero-point energy, absent in classical harmonic oscillators. Understanding these differences is essential for applications in quantum mechanics, molecular vibrations, and quantum computing technologies.
quantum oscillator vs harmonic oscillator Infographic
 electrown.com
electrown.com