Convolutional code processes data streams continuously, providing robust error correction ideal for real-time communication, while block code works on fixed-size data blocks, offering simplicity and ease of implementation. Explore the key differences between these coding techniques to understand which suits Your digital communication needs.
Table of Comparison
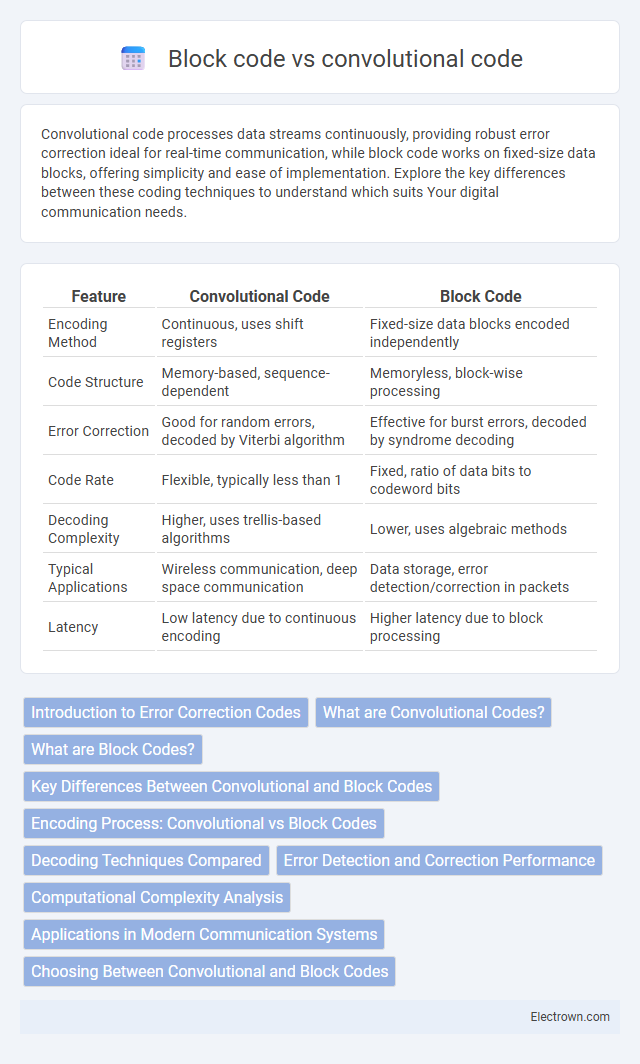
| Feature | Convolutional Code | Block Code |
|---|---|---|
| Encoding Method | Continuous, uses shift registers | Fixed-size data blocks encoded independently |
| Code Structure | Memory-based, sequence-dependent | Memoryless, block-wise processing |
| Error Correction | Good for random errors, decoded by Viterbi algorithm | Effective for burst errors, decoded by syndrome decoding |
| Code Rate | Flexible, typically less than 1 | Fixed, ratio of data bits to codeword bits |
| Decoding Complexity | Higher, uses trellis-based algorithms | Lower, uses algebraic methods |
| Typical Applications | Wireless communication, deep space communication | Data storage, error detection/correction in packets |
| Latency | Low latency due to continuous encoding | Higher latency due to block processing |
Introduction to Error Correction Codes
Error correction codes such as convolutional codes and block codes are essential for ensuring data reliability in digital communication systems. Convolutional codes process data streams by generating parity bits based on a sliding window of input bits, allowing continuous error detection and correction with techniques like the Viterbi algorithm. In contrast, block codes divide data into fixed-size blocks and append redundant bits for error detection and correction, commonly using algorithms like Reed-Solomon or Hamming codes for structured error correction within each data block.
What are Convolutional Codes?
Convolutional codes are error-correcting codes that encode data by passing it through a finite-state shift register, generating output bits based on current and previous input bits. These codes are commonly used in real-time applications such as satellite communication and mobile networks due to their ability to provide continuous error correction. Unlike block codes, convolutional codes produce encoded streams with memory, allowing the decoder to utilize algorithms like the Viterbi algorithm for optimal error correction performance.
What are Block Codes?
Block codes are a type of error-correcting code that divides the input data into fixed-size blocks and adds redundant bits to each block for error detection and correction. These codes operate on discrete blocks of data independently, allowing for simple encoding and decoding processes that enhance data reliability in communication systems. Your data integrity improves when using block codes, especially in environments prone to noise and transmission errors.
Key Differences Between Convolutional and Block Codes
Convolutional codes encode data sequentially by applying a sliding window over the input stream, generating output bits that depend on current and previous input bits, whereas block codes process fixed-size blocks of data independently, producing error-correcting codewords for each block. Convolutional codes are well-suited for continuous data transmission with efficient decoding algorithms like Viterbi, while block codes often use algebraic structures enabling simpler error detection and correction within discrete data units. The primary difference lies in the code structure and memory use: convolutional codes incorporate memory across bits, enhancing performance in noisy channels, whereas block codes operate statically on individual data blocks without inter-bit dependency.
Encoding Process: Convolutional vs Block Codes
Convolutional codes encode data by passing input bits through shift registers and combining them using modulo-2 addition, resulting in continuous output streams dependent on current and previous input bits. Block codes segment data into fixed-size blocks and encode each block independently using predefined generator matrices, producing fixed-length coded blocks. The convolutional encoding process offers memory-based encoding suited for sequential data, while block encoding processes discrete data units with simpler, parallelizable structures.
Decoding Techniques Compared
Convolutional codes are typically decoded using the Viterbi algorithm, which efficiently finds the most likely transmitted sequence by leveraging the code's trellis structure and maximizing the likelihood metric. Block codes often utilize syndrome decoding or Maximum Likelihood Decoding (MLD) methods, with algorithms like Berlekamp-Massey or Chase decoding for correcting errors within fixed-length codewords. The Viterbi algorithm offers optimal decoding for convolutional codes with manageable complexity, whereas block codes rely on algebraic techniques and syndrome calculation for error correction, reflecting different trade-offs in decoding latency and computational requirements.
Error Detection and Correction Performance
Convolutional codes provide superior error correction performance for continuous data streams by using memory elements to encode the input, enabling effective correction of burst errors through techniques like Viterbi decoding. Block codes, such as Hamming or Reed-Solomon codes, are optimized for fixed-length data blocks, offering robust error detection and correction capabilities with simpler decoding algorithms but potentially less efficiency on long sequences. The choice between convolutional and block codes depends on the application's requirements for latency, error patterns, and computational resources.
Computational Complexity Analysis
Convolutional codes typically exhibit lower decoding latency but higher computational complexity per bit compared to block codes due to their continuous data processing and reliance on algorithms like the Viterbi decoder. Block codes, such as Reed-Solomon or BCH codes, involve processing fixed-size data blocks with often simpler encoding and decoding steps, resulting in predictable but sometimes higher overall complexity for large data volumes. Your choice between convolutional and block codes should consider the trade-off between real-time decoding requirements and available computational resources, given the distinct complexity profiles of each coding scheme.
Applications in Modern Communication Systems
Convolutional codes are widely used in real-time error correction for streaming data in wireless communication and deep-space telemetry, offering continuous encoding suitable for dynamic channels. Block codes find applications in data storage systems and digital broadcasting, providing error detection and correction through fixed-size data blocks. Your choice between these codes depends on system requirements like latency, complexity, and error resilience in modern communication networks.
Choosing Between Convolutional and Block Codes
Choosing between convolutional and block codes depends on your communication system's requirements for error correction and complexity. Convolutional codes excel in continuous data streams with strong error correction capabilities using Viterbi decoding, suitable for real-time applications. Block codes, such as Reed-Solomon or Hamming codes, offer simpler encoding and decoding processes, ideal for data packets with burst error correction needs.
Convolutional code vs block code Infographic
 electrown.com
electrown.com