Short float arithmetic offers faster computations with limited precision, ideal for applications where speed is critical but minor accuracy loss is acceptable. Your understanding of when to use fixed-point arithmetic, which provides higher precision and better control over rounding errors, can significantly impact system performance; explore the rest of the article to master these crucial differences.
Table of Comparison
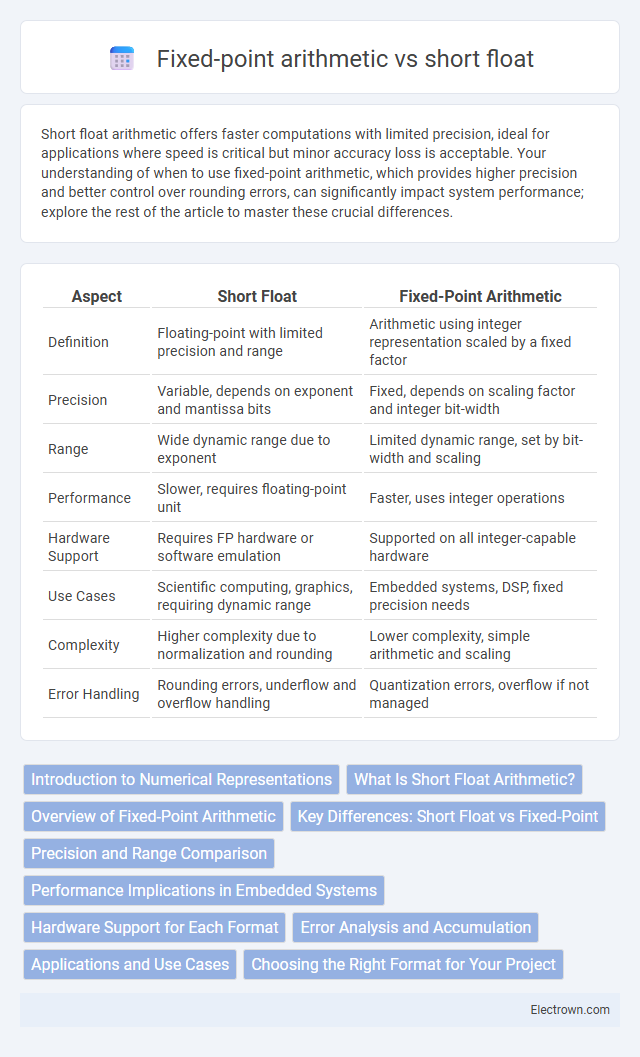
| Aspect | Short Float | Fixed-Point Arithmetic |
|---|---|---|
| Definition | Floating-point with limited precision and range | Arithmetic using integer representation scaled by a fixed factor |
| Precision | Variable, depends on exponent and mantissa bits | Fixed, depends on scaling factor and integer bit-width |
| Range | Wide dynamic range due to exponent | Limited dynamic range, set by bit-width and scaling |
| Performance | Slower, requires floating-point unit | Faster, uses integer operations |
| Hardware Support | Requires FP hardware or software emulation | Supported on all integer-capable hardware |
| Use Cases | Scientific computing, graphics, requiring dynamic range | Embedded systems, DSP, fixed precision needs |
| Complexity | Higher complexity due to normalization and rounding | Lower complexity, simple arithmetic and scaling |
| Error Handling | Rounding errors, underflow and overflow handling | Quantization errors, overflow if not managed |
Introduction to Numerical Representations
Short float and fixed-point arithmetic are fundamental numerical representations in computing, with short float using a truncated floating-point format that balances range and precision, while fixed-point represents numbers with a predetermined number of decimal places for consistent accuracy. Short floats provide dynamic scaling suitable for applications requiring a wide range of values, whereas fixed-point arithmetic is optimal for embedded systems prioritizing speed and resource efficiency. Understanding these differences enables you to select the appropriate numerical representation for precision, performance, and memory constraints in your computational tasks.
What Is Short Float Arithmetic?
Short float arithmetic uses floating-point numbers with reduced precision to save memory and increase computational speed, typically involving 16-bit or 24-bit formats instead of standard 32-bit floats. Your applications with limited resources or requiring faster calculations can benefit from short float by balancing accuracy and performance. Fixed-point arithmetic, in contrast, represents numbers with fixed decimal places, offering deterministic precision but often less flexibility in dynamic range compared to short float arithmetic.
Overview of Fixed-Point Arithmetic
Fixed-point arithmetic represents numbers using a fixed number of digits after the decimal point, allowing efficient and precise computations in embedded systems and digital signal processing. It stores values as integers scaled by a fixed factor, eliminating the overhead of floating-point hardware and reducing computational complexity. Fixed-point arithmetic is ideal for applications requiring predictable performance and low power consumption, such as real-time control systems and audio processing.
Key Differences: Short Float vs Fixed-Point
Short float and fixed-point arithmetic differ primarily in representation and precision; short float uses a floating-point format with limited bits for the exponent and mantissa to handle a wide dynamic range, while fixed-point employs a fixed number of bits for the integer and fractional parts, providing consistent precision. Short float enables efficient computation of very small or large numbers but may suffer from rounding errors and hardware complexity. Fixed-point arithmetic offers faster computation and simpler hardware design, ideal for applications requiring predictable and accurate fractional calculations within a constrained numeric range.
Precision and Range Comparison
Fixed-point arithmetic offers consistent precision by allocating a predetermined number of bits to the fractional part, making it ideal for applications requiring accurate decimal representation within a limited range. Short float, typically represented by 16-bit floating-point format, provides a wider dynamic range but sacrifices some precision due to its limited mantissa bits. When comparing precision and range, fixed-point excels in exactness for small-scale values, whereas short float accommodates a broader range with approximate accuracy.
Performance Implications in Embedded Systems
Short float arithmetic offers faster computation and reduced memory usage in embedded systems with limited resources, enabling efficient execution of real-time tasks. Fixed-point arithmetic provides predictable performance and lower power consumption due to its simpler hardware implementation, making it ideal for deterministic control algorithms. Choosing between short float and fixed-point depends on the specific embedded application requirements, such as precision, speed, and hardware constraints.
Hardware Support for Each Format
Fixed-point arithmetic benefits from widespread hardware support in microcontrollers and DSPs, enabling efficient and low-latency calculations with minimal power consumption. Short float, or half-precision floating-point format, is supported by modern GPUs and some CPUs with dedicated floating-point units (FPUs) designed for accelerated processing of smaller floating-point numbers. Specialized instructions and hardware pipelines optimize fixed-point calculations for embedded systems, whereas short float hardware support targets high-throughput applications requiring moderate dynamic range and precision.
Error Analysis and Accumulation
Short float arithmetic, often using limited precision formats like 16-bit floating point, introduces rounding errors that accumulate rapidly in iterative calculations due to lower mantissa bits, affecting the accuracy of your results. Fixed-point arithmetic can provide more predictable error bounds by representing numbers with a fixed number of fractional bits, limiting the propagation of quantization errors in repeated operations. Understanding the trade-off between short float's dynamic range and fixed-point's consistency in error accumulation is crucial for selecting the optimal format for applications requiring precise numerical stability.
Applications and Use Cases
Short float arithmetic excels in applications requiring dynamic range and precision, such as graphics rendering, scientific simulations, and machine learning models where real-time floating-point calculations are crucial. Fixed-point arithmetic is preferred in embedded systems, digital signal processing, and financial computations where predictable, low-latency performance and fixed precision enable efficient hardware implementation. Your choice between short float and fixed-point arithmetic depends on balancing precision needs, computational complexity, and resource constraints within the target application.
Choosing the Right Format for Your Project
Selecting the ideal numerical format hinges on precision and performance requirements; short float excels in dynamic range and memory efficiency for graphics and simple calculations, while fixed-point arithmetic offers deterministic behavior and faster computation in embedded systems with limited resources. Evaluate the application's tolerance for rounding errors and real-time constraints--fixed-point suits financial and control systems demanding consistent accuracy, whereas short float benefits scientific simulations needing broader scale coverage. Assess hardware capabilities and software support to optimize speed and power consumption aligned with project specifications.
Short float vs fixed-point arithmetic Infographic
 electrown.com
electrown.com