Quantum Fisher Information (QFI) extends the classical Fisher Information by incorporating the principles of quantum mechanics to determine the ultimate precision limits in parameter estimation problems involving quantum states. Understanding the differences between QFI and classical Fisher Information is essential for enhancing Your measurement accuracy in quantum technologies--explore the full article to dive deeper into their comparative roles and applications.
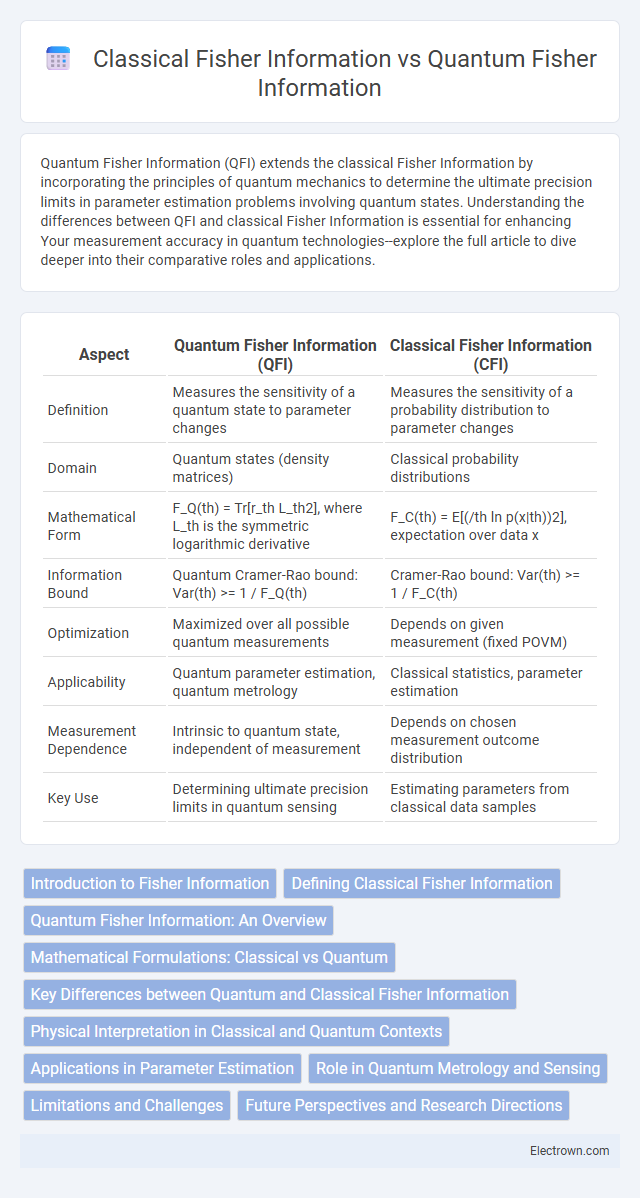
Table of Comparison
| Aspect | Quantum Fisher Information (QFI) | Classical Fisher Information (CFI) |
|---|---|---|
| Definition | Measures the sensitivity of a quantum state to parameter changes | Measures the sensitivity of a probability distribution to parameter changes |
| Domain | Quantum states (density matrices) | Classical probability distributions |
| Mathematical Form | F_Q(th) = Tr[r_th L_th2], where L_th is the symmetric logarithmic derivative | F_C(th) = E[(/th ln p(x|th))2], expectation over data x |
| Information Bound | Quantum Cramer-Rao bound: Var(th) >= 1 / F_Q(th) | Cramer-Rao bound: Var(th) >= 1 / F_C(th) |
| Optimization | Maximized over all possible quantum measurements | Depends on given measurement (fixed POVM) |
| Applicability | Quantum parameter estimation, quantum metrology | Classical statistics, parameter estimation |
| Measurement Dependence | Intrinsic to quantum state, independent of measurement | Depends on chosen measurement outcome distribution |
| Key Use | Determining ultimate precision limits in quantum sensing | Estimating parameters from classical data samples |
Introduction to Fisher Information
Fisher Information quantifies the amount of information that an observable random variable carries about an unknown parameter, crucial in parameter estimation. Classical Fisher Information applies to probability distributions derived from measurement outcomes, while Quantum Fisher Information extends this concept by considering the full quantum state, offering a fundamental bound on precision through the quantum Cramer-Rao inequality. Understanding these distinctions helps you optimize measurement strategies for enhanced parameter estimation in quantum systems.
Defining Classical Fisher Information
Classical Fisher Information measures the amount of information that an observable random variable carries about an unknown parameter upon which the probability distribution depends. It quantifies the sensitivity of the likelihood function to changes in the parameter, expressed mathematically as the expected value of the squared score function. In parameter estimation, Classical Fisher Information sets a lower bound on the variance of unbiased estimators through the Cramer-Rao inequality.
Quantum Fisher Information: An Overview
Quantum Fisher Information (QFI) quantifies the sensitivity of a quantum state to changes in a parameter, providing a fundamental limit for parameter estimation in quantum systems. Unlike classical Fisher Information, which applies to probability distributions from measurements, QFI incorporates the full quantum state, capturing both classical and quantum uncertainties. Your ability to leverage QFI enhances precision in tasks such as quantum metrology and parameter estimation beyond classical bounds.
Mathematical Formulations: Classical vs Quantum
Classical Fisher information quantifies the amount of information that an observable random variable carries about an unknown parameter, defined as the expectation of the squared score function derived from the likelihood function. Quantum Fisher information generalizes this concept to quantum systems by replacing probability distributions with density operators and employing the symmetric logarithmic derivative (SLD) to capture parameter sensitivity within quantum states. The quantum Fisher information matrix provides a tighter bound in parameter estimation, reflecting fundamental quantum limits as described by the quantum Cramer-Rao bound.
Key Differences between Quantum and Classical Fisher Information
Quantum Fisher information extends classical Fisher information by capturing the maximum information obtainable from quantum states through optimal measurements, while classical Fisher information is limited to probability distributions derived from fixed measurements. Quantum Fisher information incorporates the effects of superposition and entanglement, enabling more precise parameter estimation in quantum systems. Your ability to leverage quantum Fisher information can significantly enhance sensitivity in quantum metrology compared to classical approaches.
Physical Interpretation in Classical and Quantum Contexts
Quantum Fisher information quantifies the maximum precision achievable in estimating a parameter embedded in a quantum state, reflecting the intrinsic sensitivity of the state's probability amplitudes to parameter changes. Classical Fisher information measures the sensitivity of classical probability distributions to parameter variations, representing the information extractable from measurement outcomes. In quantum contexts, the non-commutative structure and superposition principles enable higher estimation precision than classical Fisher information limits, highlighting fundamental differences in information geometry between classical and quantum systems.
Applications in Parameter Estimation
Quantum Fisher information provides a fundamental limit on the precision of parameter estimation in quantum systems, outperforming classical Fisher information under optimal measurement strategies. It plays a crucial role in quantum metrology, enabling enhanced sensitivity in applications such as phase estimation, frequency measurement, and gravitational wave detection. Classical Fisher information remains essential in classical signal processing and statistical estimation but is bounded by quantum Fisher information when quantum resources are exploited.
Role in Quantum Metrology and Sensing
Quantum Fisher information (QFI) quantifies the ultimate precision limit in estimating parameters encoded in quantum states, surpassing classical Fisher information (CFI) by exploiting quantum coherence and entanglement. In quantum metrology and sensing, QFI determines the best possible sensitivity achievable with quantum measurement strategies, guiding the design of optimal protocols for parameter estimation. Your ability to harness QFI enables improvements in precision beyond classical limits, critical for advanced technologies like atomic clocks, gravitational wave detectors, and quantum imaging.
Limitations and Challenges
Quantum Fisher information faces limitations due to the complexity of quantum state preparation and measurement constraints, which can introduce noise and reduce estimation precision. Classical Fisher information is restricted by the intrinsic assumption of classical probability distributions, leading to less accurate parameter estimation when quantum effects are significant. Both frameworks encounter challenges in scalability and practical implementation for high-dimensional systems, impacting real-world applications in quantum metrology.
Future Perspectives and Research Directions
Quantum Fisher information offers unprecedented precision limits in parameter estimation beyond classical Fisher information, paving the way for advancements in quantum metrology and sensing technologies. Future research focuses on optimizing quantum algorithms and noise-resilient protocols to harness quantum advantages in real-world applications. Your understanding of these emerging techniques will be crucial in driving innovations in high-precision measurements and quantum computing.
quantum Fisher information vs classical Fisher information Infographic
 electrown.com
electrown.com