Decoherence-free subspaces are specific multi-qubit states immune to certain types of noise, enabling error-resistant quantum information storage, whereas protected qubits utilize error correction codes or physical encodings to shield quantum information from decoherence. Discover how these approaches differ and which might best enhance Your quantum computing system by exploring the rest of this article.
Table of Comparison
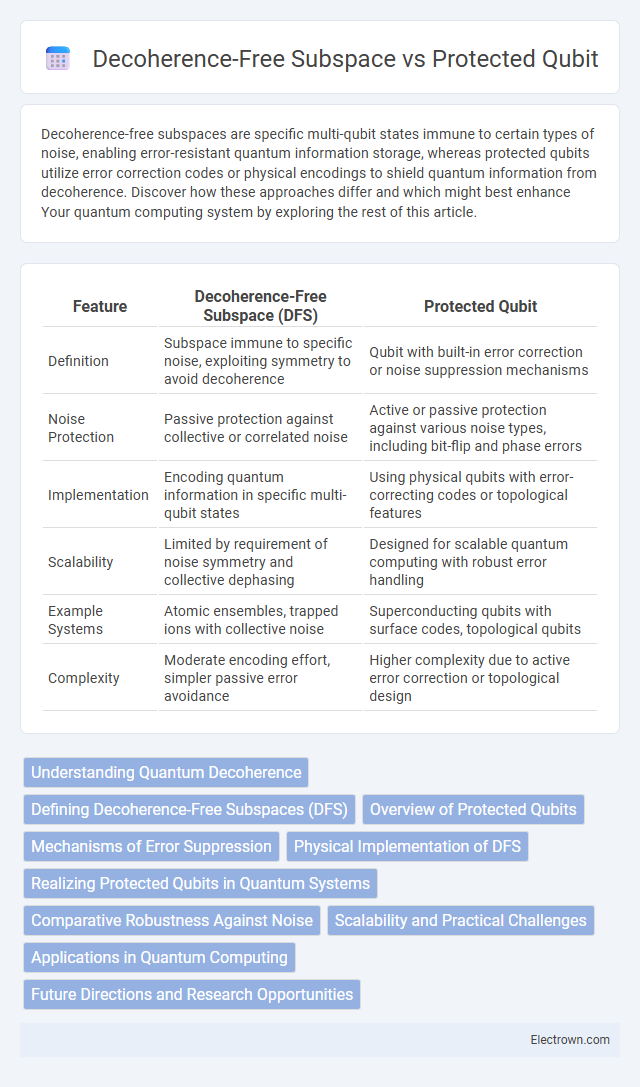
| Feature | Decoherence-Free Subspace (DFS) | Protected Qubit |
|---|---|---|
| Definition | Subspace immune to specific noise, exploiting symmetry to avoid decoherence | Qubit with built-in error correction or noise suppression mechanisms |
| Noise Protection | Passive protection against collective or correlated noise | Active or passive protection against various noise types, including bit-flip and phase errors |
| Implementation | Encoding quantum information in specific multi-qubit states | Using physical qubits with error-correcting codes or topological features |
| Scalability | Limited by requirement of noise symmetry and collective dephasing | Designed for scalable quantum computing with robust error handling |
| Example Systems | Atomic ensembles, trapped ions with collective noise | Superconducting qubits with surface codes, topological qubits |
| Complexity | Moderate encoding effort, simpler passive error avoidance | Higher complexity due to active error correction or topological design |
Understanding Quantum Decoherence
Quantum decoherence represents a major challenge in preserving the integrity of quantum information, as it causes qubits to lose coherence through environmental interactions. Decoherence-free subspaces (DFS) exploit symmetry properties of the quantum system's interaction with the environment to isolate specific states immune to certain types of noise. Protected qubits use active error correction or intrinsic hardware design to maintain coherence, offering an alternative approach to preserving your quantum information in practical quantum computing applications.
Defining Decoherence-Free Subspaces (DFS)
Decoherence-Free Subspaces (DFS) are specific subspaces of a quantum system's Hilbert space where quantum information is inherently protected from environmental noise, enabling robust quantum computation without active error correction. Unlike general protected qubits, DFS exploits symmetry in noise processes, ensuring that certain collective errors act trivially within these subspaces, preserving coherence. Your quantum information encoded in a DFS remains resilient against specific types of decoherence, making it a powerful tool for maintaining quantum state fidelity.
Overview of Protected Qubits
Protected qubits leverage physical systems or engineered environments to inherently resist decoherence by utilizing error correction codes, topological features, or noise suppression mechanisms. Decoherence-free subspaces (DFS) exploit symmetries in the system-environment interaction to isolate quantum information from noise without active correction, forming a special class of protected qubits. The main difference lies in DFS relying on passive protection through symmetry, while other protected qubits often combine passive and active strategies to maintain coherence.
Mechanisms of Error Suppression
Decoherence-free subspaces (DFS) suppress errors by encoding quantum information into subspaces immune to specific environmental noise, leveraging symmetry properties to avoid decoherence. Protected qubits, such as topological qubits, utilize physical systems with intrinsic fault tolerance, where quantum states are encoded nonlocally to resist local perturbations and noise. Your choice between DFS and protected qubits depends on the noise model and hardware constraints, as each mechanism offers unique strategies for error suppression in quantum computing.
Physical Implementation of DFS
Decoherence-free subspaces (DFS) are physically implemented by encoding quantum information into subspaces of multi-qubit systems that are invariant under specific noise operators, often using collective interactions in trapped ions, superconducting qubits, or photonic systems to exploit symmetry properties. Protected qubits, on the other hand, involve hardware-level designs such as topological qubits or error-correcting codes that inherently resist decoherence through physical isolation or constant active error correction protocols. Experimental realization of DFS typically requires precise control of qubit coupling and noise correlation, while protected qubits rely on engineered materials and architectures to maintain coherence over longer timescales.
Realizing Protected Qubits in Quantum Systems
Decoherence-free subspaces (DFS) leverage symmetry properties of quantum noise to isolate qubits from environmental decoherence, enhancing coherence times without active error correction. Protected qubits employ engineered interactions and energy gaps to suppress errors, often combining DFS principles with topological or bosonic codes for robust quantum information storage. Realizing protected qubits involves precise control of system Hamiltonians and environmental couplings to create stable subspaces that maintain quantum coherence for fault-tolerant quantum computing.
Comparative Robustness Against Noise
Decoherence-free subspaces (DFS) achieve robustness against noise by isolating qubits from collective errors via symmetry properties, effectively nullifying certain types of environmental interactions. Protected qubits, such as those implemented using topological codes or dynamical decoupling, leverage intrinsic error suppression mechanisms or active error correction to maintain coherence under a broader range of noise models. Your quantum system benefits from selecting a method aligned with its noise characteristics, where DFS excels against correlated noise, while protected qubits offer enhanced resilience to more general and independent error processes.
Scalability and Practical Challenges
Decoherence-free subspaces offer scalability advantages by enabling multiple qubits to be encoded in collective states resistant to specific noise types, reducing error rates without extensive error correction overhead. Protected qubits such as topological or Majorana qubits provide inherent fault tolerance through physical protection mechanisms but face significant fabrication and control challenges that limit near-term scalability. Practical implementation hurdles for decoherence-free subspaces include identifying suitable symmetry conditions and maintaining system coherence, while protected qubits require advanced materials and precise manipulation techniques, impacting their immediate scalability potential.
Applications in Quantum Computing
Decoherence-free subspaces (DFS) offer a robust method for preserving quantum information by encoding qubits in states immune to certain environmental noise, enhancing fault-tolerant quantum computing. Protected qubits, such as topological qubits, leverage intrinsic physical properties to suppress errors at the hardware level, providing a scalable approach to quantum error correction. Understanding these advanced quantum error mitigation techniques is essential for improving the stability and reliability of Your quantum computing applications.
Future Directions and Research Opportunities
Future research on decoherence-free subspaces (DFS) aims to enhance error correction capabilities by integrating DFS with dynamical decoupling and quantum error-correcting codes for robust qubit protection. Advances in protected qubit architectures, such as topological qubits and cat states, focus on improving coherence times and scalability in noisy quantum environments. Exploring hybrid approaches that combine DFS and protected qubits presents promising opportunities for developing fault-tolerant quantum computing systems.
decoherence-free subspace vs protected qubit Infographic
 electrown.com
electrown.com