Geometric phase arises from the evolution of a quantum system's state along a specific path in parameter space, independent of the system's energy, while dynamical phase depends directly on the time integral of the system's energy. Understanding these distinctions can enhance your grasp of quantum mechanics and inspire you to explore the detailed comparison in the rest of the article.
Table of Comparison
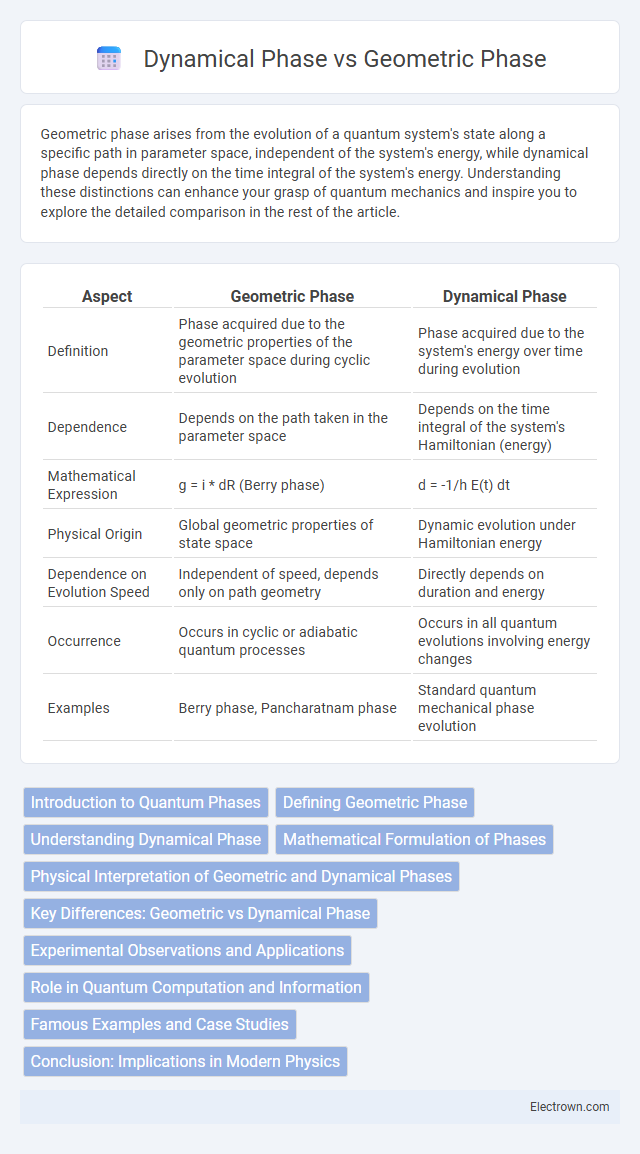
| Aspect | Geometric Phase | Dynamical Phase |
|---|---|---|
| Definition | Phase acquired due to the geometric properties of the parameter space during cyclic evolution | Phase acquired due to the system's energy over time during evolution |
| Dependence | Depends on the path taken in the parameter space | Depends on the time integral of the system's Hamiltonian (energy) |
| Mathematical Expression | g = i |
d = -1/h E(t) dt |
| Physical Origin | Global geometric properties of state space | Dynamic evolution under Hamiltonian energy |
| Dependence on Evolution Speed | Independent of speed, depends only on path geometry | Directly depends on duration and energy |
| Occurrence | Occurs in cyclic or adiabatic quantum processes | Occurs in all quantum evolutions involving energy changes |
| Examples | Berry phase, Pancharatnam phase | Standard quantum mechanical phase evolution |
Introduction to Quantum Phases
Quantum phases arise from the evolution of quantum states, where the dynamical phase depends on the energy and time of evolution, reflecting the system's dynamical properties. The geometric phase, also known as the Berry phase, depends solely on the path taken by the quantum state in parameter space, independent of time and energy, revealing underlying geometric and topological features. Understanding these phases is crucial for precise control in quantum computing and quantum information processing, where your manipulation of quantum states leverages both dynamic and geometric contributions.
Defining Geometric Phase
Geometric phase refers to a phase difference acquired over the course of a cycle, resulting from the system's geometry or parameter space rather than its energy or time evolution. Unlike dynamical phase, which depends on the time integral of the system's energy, the geometric phase depends solely on the path taken by the system in its parameter space. Understanding the geometric phase can enhance your ability to analyze quantum systems, enabling insights beyond conventional dynamical behavior.
Understanding Dynamical Phase
Dynamical phase represents the accumulated phase shift of a quantum system due to the energy eigenvalues and the elapsed time, described mathematically by the integral of the system's instantaneous energy over time. It depends directly on the Hamiltonian and the duration of the evolution, capturing the energy-driven evolution of quantum states. Unlike geometric phase, dynamical phase varies with changes in the system's energy or evolution time and lacks topological or path-dependent properties.
Mathematical Formulation of Phases
The geometric phase is mathematically formulated through the integral of the Berry connection over a parameter space, capturing the holonomy of the quantum state's evolution path, often represented as \(\gamma = \oint_C \mathbf{A} \cdot d\mathbf{R}\). The dynamical phase, in contrast, is derived from the time integral of the Hamiltonian's instantaneous eigenvalue, expressed as \(\delta = -\frac{1}{\hbar} \int_0^T E(t) dt\), reflecting the energy-time evolution of your quantum system. Understanding these formulations allows precise manipulation of phase factors in quantum computation and interferometric setups.
Physical Interpretation of Geometric and Dynamical Phases
The geometric phase arises from the global properties of the parameter space path traced by a quantum system's state, reflecting purely geometric aspects independent of the Hamiltonian's energy eigenvalues. In contrast, the dynamical phase depends explicitly on the time integral of the system's instantaneous energy, representing the total accumulated action due to Hamiltonian evolution. This distinction highlights that while the dynamical phase accounts for energy-driven temporal evolution, the geometric phase encodes topological information related to the system's trajectory in Hilbert space.
Key Differences: Geometric vs Dynamical Phase
Geometric phase arises from the global properties of a system's parameter space and depends solely on the path taken during cyclic evolution, while the dynamical phase is determined by the time integral of the system's energy, reflecting the duration and energy of the process. Geometric phase is independent of the speed of evolution and captures topological aspects, whereas dynamical phase changes with time and energy variations. Key differences highlight that geometric phase provides insight into intrinsic system geometry, contrasting with dynamical phase's sensitivity to temporal dynamics.
Experimental Observations and Applications
Experimental observations of geometric phase reveal its robustness against certain types of noise, distinguishing it from the dynamical phase that depends directly on energy and time. Applications in quantum computing exploit the geometric phase for fault-tolerant quantum gates, while precision measurement techniques use dynamical phase variations for sensitive parameter estimation. Your ability to manipulate these phases enables advancements in topological quantum systems and interferometry.
Role in Quantum Computation and Information
Geometric phase plays a crucial role in quantum computation by offering robust, fault-tolerant quantum gates less susceptible to certain types of errors compared to dynamical phase gates, which rely on energy-level differences and are sensitive to fluctuations in system parameters. Your understanding of these phases enables the design of quantum algorithms that exploit geometric phase properties to improve coherence and gate fidelity, essential for reliable quantum information processing. Leveraging geometric phases enhances the resilience of quantum circuits against noise, advancing scalable quantum computing technologies.
Famous Examples and Case Studies
The Aharonov-Bohm effect demonstrates the geometric phase through phase shifts in electron wavefunctions influenced by electromagnetic potentials in regions with zero magnetic fields. In contrast, the dynamical phase is exemplified in simple harmonic oscillators where energy eigenvalues dictate the time evolution of quantum states. Another renowned case is the Berry phase observed in cyclic adiabatic processes, highlighting the geometric phase's dependence solely on the pathway traversed in parameter space rather than on time or energy.
Conclusion: Implications in Modern Physics
Geometric phase and dynamical phase represent distinct contributions to the total phase in quantum systems, with geometric phase arising from the system's path in parameter space and dynamical phase depending on energy and time. The geometric phase plays a crucial role in modern physics applications such as quantum computing, topological materials, and interference phenomena, offering robustness against certain types of errors. Understanding these phase differences enhances precision measurement techniques and drives advances in quantum information processing and condensed matter physics.
geometric phase vs dynamical phase Infographic
 electrown.com
electrown.com