The Landauer limit defines the minimum possible amount of energy required to erase one bit of information, grounded in thermodynamics and information theory, while the Heisenberg limit pertains to the precision bounds of measurements dictated by quantum mechanics. Understanding how these fundamental physical limits interact can reveal profound insights into the constraints of computing and measurement technologies; explore the rest of this article to learn more about their implications for Your future innovations.
Table of Comparison
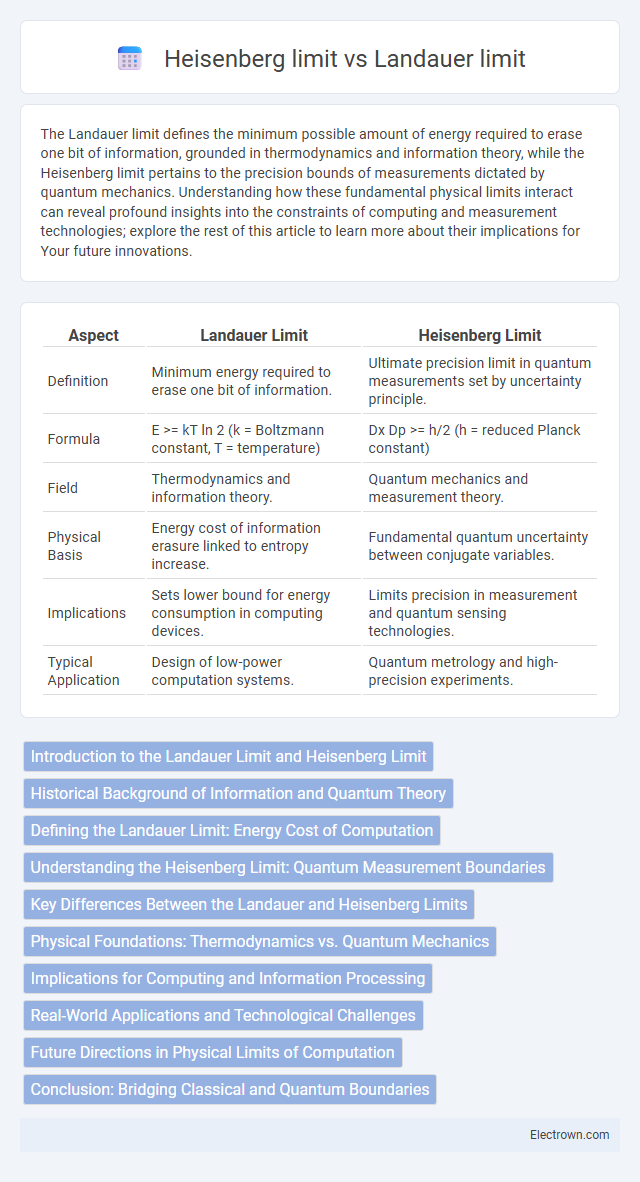
| Aspect | Landauer Limit | Heisenberg Limit |
|---|---|---|
| Definition | Minimum energy required to erase one bit of information. | Ultimate precision limit in quantum measurements set by uncertainty principle. |
| Formula | E >= kT ln 2 (k = Boltzmann constant, T = temperature) | Dx Dp >= h/2 (h = reduced Planck constant) |
| Field | Thermodynamics and information theory. | Quantum mechanics and measurement theory. |
| Physical Basis | Energy cost of information erasure linked to entropy increase. | Fundamental quantum uncertainty between conjugate variables. |
| Implications | Sets lower bound for energy consumption in computing devices. | Limits precision in measurement and quantum sensing technologies. |
| Typical Application | Design of low-power computation systems. | Quantum metrology and high-precision experiments. |
Introduction to the Landauer Limit and Heisenberg Limit
The Landauer Limit defines the minimum possible energy required to erase one bit of information, establishing a fundamental thermodynamic bound in computation at approximately kT ln(2) joules per bit, where k is the Boltzmann constant and T is temperature. The Heisenberg Limit, rooted in quantum mechanics, sets the ultimate precision boundary for measurements, such as phase estimation, based on the uncertainty principle and scales inversely with the total measurement resources like time or number of particles. Both limits serve as benchmark constraints in information theory and quantum measurement, impacting the fields of computational thermodynamics and quantum metrology.
Historical Background of Information and Quantum Theory
The Landauer limit, established by Rolf Landauer in 1961, quantifies the minimum energy required to erase a single bit of information, linking thermodynamics with information theory. Heisenberg's uncertainty principle, formulated by Werner Heisenberg in 1927, sets fundamental quantum limits on the precision of simultaneous measurements of conjugate variables, influencing the understanding of quantum measurement limits. Both concepts emerged from pivotal shifts in 20th-century physics, integrating information concepts with thermodynamics and quantum mechanics respectively.
Defining the Landauer Limit: Energy Cost of Computation
The Landauer limit defines the minimum possible amount of energy required to erase one bit of information, quantified as kT ln(2), where k is the Boltzmann constant and T is the temperature of the computing environment. This fundamental thermodynamic limit sets a baseline for energy efficiency in classical computation, emphasizing the intrinsic cost of bit erasure linked to entropy increase. In contrast, the Heisenberg limit pertains to measurement precision and quantum uncertainty, representing a distinct boundary in quantum mechanics unrelated to energy dissipation in classical information processing.
Understanding the Heisenberg Limit: Quantum Measurement Boundaries
The Heisenberg limit defines the fundamental quantum measurement boundary, setting the maximum precision achievable when estimating parameters such as phase or position in quantum systems, governed by the uncertainty principle. It contrasts with the Landauer limit, which establishes the minimum energy required for classical information erasure at thermodynamic equilibrium. Understanding the Heisenberg limit is crucial for optimizing quantum sensors and quantum computing accuracy, pushing beyond classical measurement constraints while respecting quantum uncertainty.
Key Differences Between the Landauer and Heisenberg Limits
The Landauer limit defines the minimum amount of energy required to erase one bit of information, establishing a thermodynamic bound based on entropy and temperature. In contrast, the Heisenberg limit arises from quantum mechanics, setting the ultimate precision bound for measurements due to the uncertainty principle. Understanding these distinct limits helps optimize Your computational efficiency by balancing energy consumption with quantum measurement constraints.
Physical Foundations: Thermodynamics vs. Quantum Mechanics
The Landauer limit, grounded in thermodynamics, defines the minimum energy required to erase one bit of information, emphasizing entropy and heat dissipation in classical systems. In contrast, the Heisenberg limit arises from quantum mechanics, setting the ultimate precision limit for measurements due to the uncertainty principle. Your understanding of computational boundaries benefits from recognizing these distinct physical foundations: thermodynamic irreversibility for Landauer and quantum uncertainty for Heisenberg.
Implications for Computing and Information Processing
The Landauer limit defines the minimum possible energy required to erase one bit of information, setting a fundamental thermodynamic bound for computing efficiency. The Heisenberg limit, derived from quantum mechanics, constrains the precision and speed of information processing by limiting how quickly quantum states can evolve, impacting the ultimate performance of quantum computers. Your ability to optimize computing technologies hinges on balancing these limits to achieve minimal energy consumption while maximizing processing speed and accuracy.
Real-World Applications and Technological Challenges
The Landauer limit defines the minimum energy required for irreversible computation, establishing a theoretical benchmark for energy-efficient data processing in semiconductor technologies and low-power computing devices. The Heisenberg limit, rooted in quantum mechanics, sets constraints on measurement precision and coherence time, impacting the design of quantum sensors and quantum computing systems that rely on minimizing decoherence and optimizing qubit control. Real-world applications confront technological challenges such as minimizing thermal noise to approach the Landauer limit and mitigating quantum decoherence to harness the Heisenberg limit, necessitating advancements in materials science, cryogenic engineering, and error-correction protocols.
Future Directions in Physical Limits of Computation
Exploring the future directions in the physical limits of computation involves understanding the Landauer limit, which sets the minimum energy required for bit erasure, and the Heisenberg limit, which constrains measurement precision based on quantum uncertainty. Advances in quantum computing and nanoscale device engineering push the boundaries closer to these fundamental limits, enabling more energy-efficient and faster computations. Your insight into these evolving principles can guide the development of technologies that balance computational speed, energy consumption, and quantum constraints.
Conclusion: Bridging Classical and Quantum Boundaries
The Landauer limit establishes the minimum energy required for classical information erasure, setting a fundamental thermodynamic bound in computation. The Heisenberg limit defines the ultimate precision in quantum measurement, constrained by the uncertainty principle, marking the quantum mechanical boundary. Bridging these limits reveals a critical intersection where classical thermodynamics meets quantum mechanics, guiding the development of energy-efficient quantum technologies and computational paradigms.
Landauer limit vs Heisenberg limit Infographic
 electrown.com
electrown.com