Phase offset refers to the difference in the initial angle between two waveforms, impacting signal alignment and timing, while frequency offset describes the discrepancy in the rate at which signals oscillate, affecting synchronization and data integrity. Understanding the distinction between phase and frequency offset is crucial for optimizing communication systems, so explore the rest of the article to enhance Your signal processing knowledge.
Table of Comparison
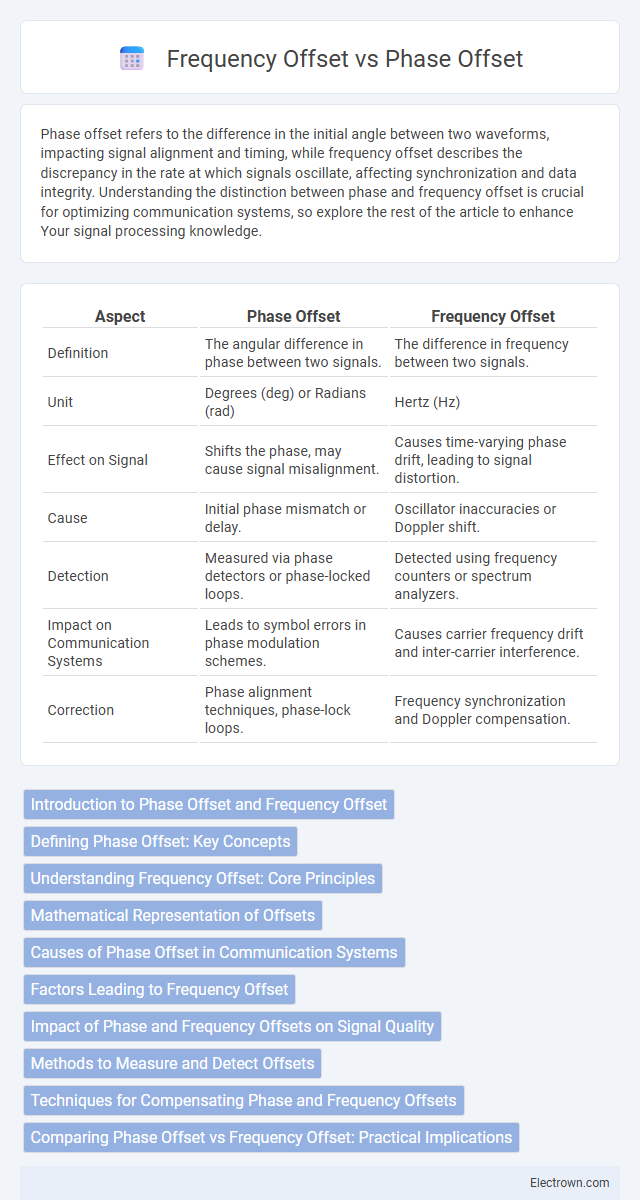
| Aspect | Phase Offset | Frequency Offset |
|---|---|---|
| Definition | The angular difference in phase between two signals. | The difference in frequency between two signals. |
| Unit | Degrees (deg) or Radians (rad) | Hertz (Hz) |
| Effect on Signal | Shifts the phase, may cause signal misalignment. | Causes time-varying phase drift, leading to signal distortion. |
| Cause | Initial phase mismatch or delay. | Oscillator inaccuracies or Doppler shift. |
| Detection | Measured via phase detectors or phase-locked loops. | Detected using frequency counters or spectrum analyzers. |
| Impact on Communication Systems | Leads to symbol errors in phase modulation schemes. | Causes carrier frequency drift and inter-carrier interference. |
| Correction | Phase alignment techniques, phase-lock loops. | Frequency synchronization and Doppler compensation. |
Introduction to Phase Offset and Frequency Offset
Phase offset refers to the angular difference between the phases of two periodic signals at a given point in time, expressed in degrees or radians, which impacts signal synchronization and modulation accuracy. Frequency offset describes the difference in frequency between a reference signal and a received signal, measured in hertz (Hz), causing issues like carrier frequency mismatch and signal distortion in communication systems. Both phase offset and frequency offset are critical parameters in wireless communication, affecting the performance of demodulation, signal detection, and overall system reliability.
Defining Phase Offset: Key Concepts
Phase offset refers to the angular difference between two periodic signals at a specific point in time, typically measured in degrees or radians. It is a crucial parameter in signal processing and communications, determining the alignment and synchronization of waveforms without affecting their frequency. Understanding phase offset helps you analyze signal phase relationships and optimize systems like phase-locked loops and coherent demodulators.
Understanding Frequency Offset: Core Principles
Frequency offset refers to the deviation between the expected carrier frequency and the actual received signal frequency, often caused by Doppler shifts or oscillator inaccuracies. Phase offset represents the initial phase difference between transmitted and received signals but remains constant over time, while frequency offset continuously causes phase drift, impacting signal demodulation. Understanding frequency offset is essential for correcting signal alignment and improving communication system performance by ensuring proper synchronization and minimizing bit errors.
Mathematical Representation of Offsets
Phase offset is mathematically represented as a constant angle shift \(\phi\) in the signal's phase term, expressed as \(x(t) = A \cos(2\pi f t + \phi)\), where \(A\) is amplitude and \(f\) is frequency. Frequency offset involves a deviation \(\Delta f\) from the nominal frequency, leading to a time-varying phase shift given by \(x(t) = A \cos(2\pi (f + \Delta f) t)\). The distinction lies in phase offset producing a fixed phase difference, while frequency offset induces a continuously increasing phase error over time due to frequency mismatch.
Causes of Phase Offset in Communication Systems
Phase offset in communication systems primarily arises from mismatches in oscillator frequencies between the transmitter and receiver, leading to phase discrepancies over time. Signal propagation delays and multipath effects cause variations in the arrival time of signal components, further contributing to phase errors. Imperfect synchronization and hardware imperfections, such as phase noise in local oscillators, also significantly impact phase offset magnitude.
Factors Leading to Frequency Offset
Frequency offset arises primarily due to discrepancies between transmitter and receiver local oscillator frequencies, leading to a shift in the carrier signal's nominal frequency. Environmental variations, such as temperature fluctuations and component aging, further contribute to the drift in oscillator stability, causing frequency misalignment. Additionally, Doppler shifts caused by relative motion between communication devices impact frequency offset, especially in mobile and satellite communications.
Impact of Phase and Frequency Offsets on Signal Quality
Phase offset causes a shift in the signal's waveform, leading to distortion and reduced signal clarity, especially in phase-sensitive modulation schemes like QPSK or QAM. Frequency offset results in a continuous rotation of the signal constellation, causing inter-carrier interference and degradation of synchronization, which severely impacts demodulation accuracy. Your communication system's signal quality deteriorates with increasing phase and frequency offsets, making precise calibration essential for optimal performance.
Methods to Measure and Detect Offsets
Phase offset measurement typically involves methods like phase-locked loops (PLLs) and vector signal analyzers that compare the phase difference between a reference signal and the test signal. Frequency offset detection commonly uses spectrum analyzers and frequency counters that identify deviations in signal frequency relative to a known carrier frequency. Advanced techniques incorporate digital signal processing algorithms, such as Fourier transform-based estimation and cross-correlation, to accurately quantify both phase and frequency offsets in communication systems.
Techniques for Compensating Phase and Frequency Offsets
Techniques for compensating phase and frequency offsets include phase-locked loops (PLLs) and frequency-locked loops (FLLs), which dynamically adjust the receiver's local oscillator to match the incoming signal. Digital signal processing algorithms such as Costas loops and extended Kalman filters provide robust estimation and correction of these offsets, enhancing signal integrity in communication systems. Your choice of compensation method depends on the system's tolerance requirements and computational resources available.
Comparing Phase Offset vs Frequency Offset: Practical Implications
Phase offset represents a constant angular displacement between two signals, causing a fixed shift in signal timing, while frequency offset involves a continuous difference in oscillation rate, resulting in progressive phase drift over time. Practically, phase offset impacts initial signal alignment and synchronization, critical in modulation schemes like QPSK, whereas frequency offset leads to cumulative errors affecting demodulation accuracy and system stability in communication receivers. Effective compensation techniques differ; phase offset requires simple phase correction, but frequency offset demands complex tracking loops such as phase-locked loops (PLLs) for real-time adjustment.
Phase Offset vs Frequency Offset Infographic
 electrown.com
electrown.com