2's complement simplifies binary subtraction by representing negative numbers with a unique zero, eliminating the ambiguity found in 1's complement which has both positive and negative zeros. Explore the rest of the article to understand how these methods impact your computing efficiency and error handling.
Table of Comparison
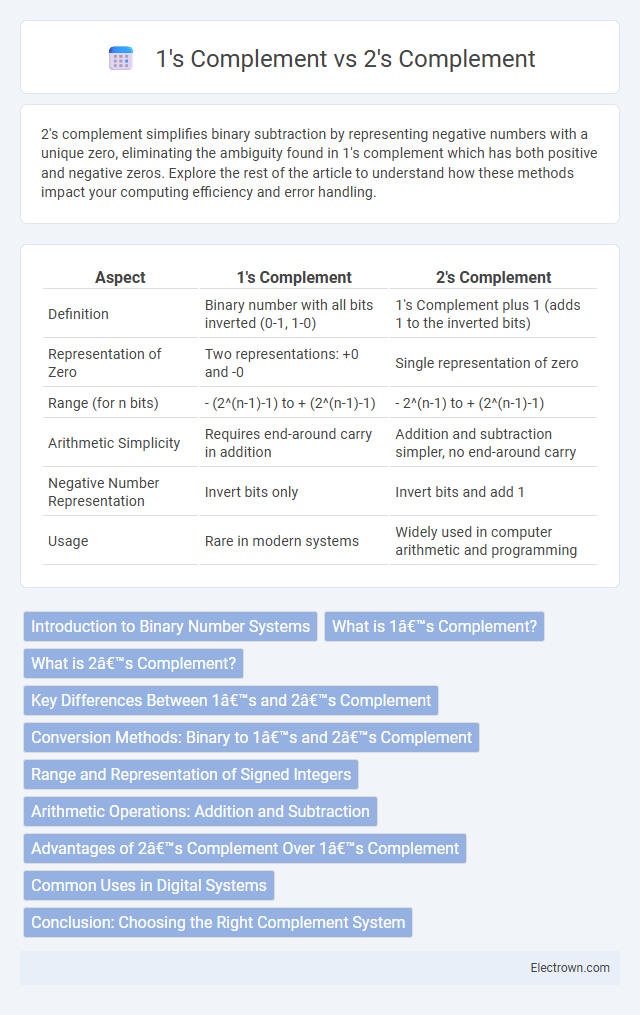
| Aspect | 1's Complement | 2's Complement |
|---|---|---|
| Definition | Binary number with all bits inverted (0-1, 1-0) | 1's Complement plus 1 (adds 1 to the inverted bits) |
| Representation of Zero | Two representations: +0 and -0 | Single representation of zero |
| Range (for n bits) | - (2^(n-1)-1) to + (2^(n-1)-1) | - 2^(n-1) to + (2^(n-1)-1) |
| Arithmetic Simplicity | Requires end-around carry in addition | Addition and subtraction simpler, no end-around carry |
| Negative Number Representation | Invert bits only | Invert bits and add 1 |
| Usage | Rare in modern systems | Widely used in computer arithmetic and programming |
Introduction to Binary Number Systems
The 2's complement and 1's complement are binary number system techniques used to represent signed integers in digital computing. 1's complement inverts all bits of the binary number, while 2's complement inverts bits and adds one to the least significant bit, simplifying arithmetic operations. 2's complement is preferred in modern systems due to its unique zero representation and straightforward binary addition, eliminating the ambiguity present in 1's complement.
What is 1’s Complement?
1's complement is a binary number representation method where each bit of a binary number is inverted, changing all 0s to 1s and all 1s to 0s, primarily used to represent negative numbers in signed binary arithmetic. It differs from 2's complement because 1's complement has two representations of zero: positive zero and negative zero, which can lead to complications in arithmetic operations. This method requires end-around carry addition for subtraction, making it less efficient than the widely adopted 2's complement system in modern computing.
What is 2’s Complement?
2's Complement is a binary representation system used to encode negative numbers by inverting all bits of a number (1's Complement) and adding one to the least significant bit. This method simplifies arithmetic operations in digital computers, allowing for straightforward addition and subtraction without separate subtraction circuitry. Your understanding of 2's Complement enhances accuracy and efficiency in computing signed integers.
Key Differences Between 1’s and 2’s Complement
1's Complement represents negative numbers by inverting all bits of the positive number, while 2's Complement adds 1 to the 1's Complement result, making it easier for arithmetic operations. The key difference lies in how zero is represented: 1's Complement has two representations of zero (positive and negative zero), whereas 2's Complement has a unique zero representation. This difference leads to simpler hardware implementation and more efficient arithmetic in 2's Complement systems, which are widely used in modern computers.
Conversion Methods: Binary to 1’s and 2’s Complement
To convert a binary number to its 1's complement, invert all the bits, changing each 0 to 1 and each 1 to 0. For 2's complement conversion, first find the 1's complement, then add 1 to the least significant bit, effectively representing negative binary values more efficiently. These methods ensure Your binary data accurately reflects signed integers in digital systems.
Range and Representation of Signed Integers
2's Complement represents signed integers with a range from -2^(n-1) to 2^(n-1)-1 for an n-bit number, allowing a single representation of zero. 1's Complement represents signed integers with a range from -(2^(n-1)-1) to 2^(n-1)-1, but it includes both positive and negative zero, leading to two different representations for zero. 2's Complement simplifies arithmetic operations and overflow detection due to its unique zero and straightforward binary addition, while 1's Complement requires end-around carry adjustment.
Arithmetic Operations: Addition and Subtraction
In 2's complement, addition and subtraction are simplified since numbers have a unique representation for zero and negative values, allowing straightforward binary addition without separate subtraction circuits. In contrast, 1's complement requires end-around carry addition for subtraction and has two representations of zero, complicating arithmetic operations and error handling. Understanding these differences helps you choose the appropriate system for efficient binary arithmetic in digital computing.
Advantages of 2’s Complement Over 1’s Complement
Two's complement offers significant advantages over one's complement, including a simpler arithmetic process since it uses a single representation for zero, eliminating the issue of positive and negative zero that complicates calculations in one's complement. This representation simplifies hardware design by allowing straightforward binary addition and subtraction without requiring end-around carry adjustments, improving both speed and efficiency. Your computing tasks benefit from reduced complexity and increased reliability when using two's complement for signed integer operations.
Common Uses in Digital Systems
In digital systems, 2's complement is commonly used for representing signed integers due to its simplicity in arithmetic operations and unique zero representation, which eliminates ambiguity. 1's complement, while historically significant, is less favored as it has two representations for zero and complicates addition with end-around carry. Your choice of complement system affects processor design, error detection, and the efficiency of computation in embedded and digital signal processing applications.
Conclusion: Choosing the Right Complement System
Choosing the right complement system depends on your application's needs for simplicity versus efficiency; 2's Complement simplifies arithmetic operations and eliminates the ambiguity of two zero representations found in 1's Complement. In digital computing, 2's Complement is preferred due to its straightforward implementation of addition and subtraction without extra logic for sign handling. Your decision should balance design complexity and performance, favoring 2's Complement for modern processors requiring reliable and efficient binary arithmetic.
2’s Complement vs 1’s Complement Infographic
 electrown.com
electrown.com