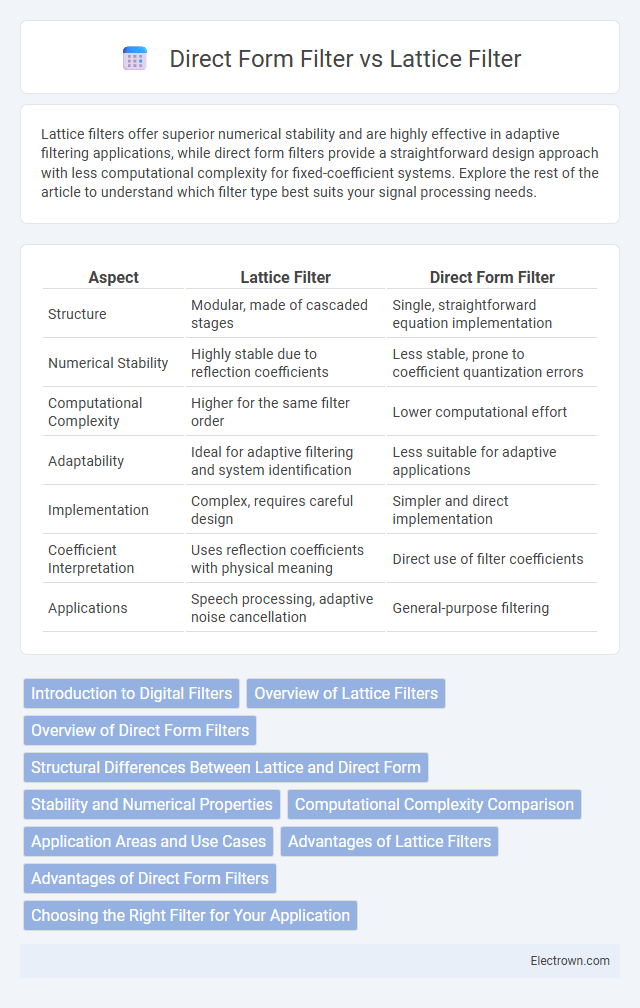
Lattice filters offer superior numerical stability and are highly effective in adaptive filtering applications, while direct form filters provide a straightforward design approach with less computational complexity for fixed-coefficient systems. Explore the rest of the article to understand which filter type best suits your signal processing needs.
Table of Comparison
| Aspect | Lattice Filter | Direct Form Filter |
|---|---|---|
| Structure | Modular, made of cascaded stages | Single, straightforward equation implementation |
| Numerical Stability | Highly stable due to reflection coefficients | Less stable, prone to coefficient quantization errors |
| Computational Complexity | Higher for the same filter order | Lower computational effort |
| Adaptability | Ideal for adaptive filtering and system identification | Less suitable for adaptive applications |
| Implementation | Complex, requires careful design | Simpler and direct implementation |
| Coefficient Interpretation | Uses reflection coefficients with physical meaning | Direct use of filter coefficients |
| Applications | Speech processing, adaptive noise cancellation | General-purpose filtering |
Introduction to Digital Filters
Digital filters are essential components in signal processing used to manipulate or enhance signals by selectively amplifying or attenuating certain frequency components. Lattice filters offer stability and numerical robustness through a modular structure ideal for adaptive filtering and speech processing, while direct form filters provide a straightforward implementation with coefficients directly shaping the input-output relationship. Choosing between lattice and direct form filters depends on factors like computational efficiency, stability requirements, and application-specific constraints.
Overview of Lattice Filters
Lattice filters provide a modular, stable structure ideal for adaptive filtering and linear predictive coding applications. Their unique wave digital nature allows for efficient numerical stability and phase equalization compared to direct form filters. You benefit from lattice filters' resistance to coefficient quantization errors, making them preferable in high-precision signal processing tasks.
Overview of Direct Form Filters
Direct Form Filters represent a fundamental structure in digital signal processing, characterized by straightforward implementation of difference equations using delay elements, multipliers, and adders. These filters are divided into Direct Form I and Direct Form II, where Direct Form II is more memory-efficient by sharing delay elements between feedforward and feedback paths. Their design simplicity allows easy realization of Infinite Impulse Response (IIR) and Finite Impulse Response (FIR) filters but may suffer from numerical instability and coefficient quantization issues in fixed-point arithmetic.
Structural Differences Between Lattice and Direct Form
Lattice filters utilize a modular, reflection coefficient-based structure that enhances numerical stability and simplifies coefficient adaptation, contrasting with direct form filters which implement a straightforward cascade of feedforward and feedback coefficients. The direct form filter's structure is more susceptible to coefficient quantization errors and instability in fixed-point implementations, whereas lattice filters better maintain performance in these scenarios due to their orthogonal characteristics. Your choice between these structures affects filter stability, implementation complexity, and robustness in signal processing applications.
Stability and Numerical Properties
Lattice filters exhibit superior numerical stability due to their inherently bounded-input bounded-output (BIBO) stable structure, making them less sensitive to coefficient quantization errors compared to direct form filters. Direct form filters often suffer from pole-zero cancellations and coefficient sensitivity that can lead to numerical instability, especially in fixed-point implementations. The recursive nature of lattice filters ensures consistent stability even under finite word-length effects, making them preferable for adaptive filtering applications.
Computational Complexity Comparison
Lattice filters typically exhibit lower computational complexity compared to direct form filters due to their efficient use of reflection coefficients, which simplifies stability control and reduces the number of multiplications and additions required. Direct form filters often involve more arithmetic operations as they rely on feedforward and feedback coefficients directly, leading to increased processing load. Your choice of filter implementation can significantly impact processing speed and resource usage, especially in real-time digital signal processing applications.
Application Areas and Use Cases
Lattice filters excel in adaptive signal processing, echo cancellation, and speech enhancement due to their numerical stability and efficient parameter estimation in time-varying systems. Direct form filters are widely used in fixed-coefficient digital filtering applications like audio equalization, control systems, and real-time finite impulse response (FIR) or infinite impulse response (IIR) filtering where straightforward implementation and minimal computational complexity are required. Both filter structures find critical roles in telecommunications, radar signal processing, and biomedical signal analysis, with the choice driven by system stability, adaptability, and computational constraints.
Advantages of Lattice Filters
Lattice filters offer superior numerical stability and are highly efficient in adaptive filtering applications due to their orthogonal structure, which minimizes sensitivity to coefficient quantization. They provide better control over reflection coefficients, enabling precise frequency response shaping and improved robustness in signal processing. Your choice of a lattice filter can enhance performance in systems requiring low computational complexity and reliable real-time updates.
Advantages of Direct Form Filters
Direct Form Filters offer a more straightforward implementation with fewer memory requirements compared to Lattice Filters, making them ideal for real-time signal processing applications. Their structure allows for easier coefficient manipulation and tuning, which enhances flexibility in filter design. You benefit from their efficiency in fixed-point arithmetic systems, reducing computational complexity while maintaining accurate frequency response.
Choosing the Right Filter for Your Application
Lattice filters provide superior numerical stability and phase linearity, making them ideal for adaptive filtering and speech processing applications. Direct form filters, offering simpler implementation and lower computational load, suit applications requiring straightforward IIR or FIR filter designs with fixed coefficients. Selecting the right filter involves balancing stability requirements, computational resources, and the specific signal characteristics of your application.
Lattice Filter vs Direct Form Filter Infographic
 electrown.com
electrown.com